
| 年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
| 需要量(万件) | 236 | 246 | 257 | 276 | 286 |
分析 (1)由所给数据看出年需求量与年份之间是近似直线上升,计算$\overline{x}$、$\overline{y}$,求出回归系数,写出回归直线方程;
(2)利用回归方程求出x=2018时$\stackrel{∧}{y}$的值即可.
解答 解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,
计算$\overline{x}$=$\frac{1}{5}$×(2008+2010+2012+2014+2016)=2012,
$\overline{y}$=$\frac{1}{5}$×(236+246+257+276+286)=260.2,
回归系数$\widehatb=\frac{{({-4})×({-24.2})+({-2})×({-14.2})+2×15.8+4×25.8}}{{{4^2}+{2^2}+{2^2}+{4^2}}}=\frac{260}{40}=6.5$,
$\widehata=\overline y-\widehatb\overline x=-12817.8$,
所以所求回归直线方程为:$\widehaty=6.5x-12817.8$;
(2)由(1)中回归方程,把x=2018代入方程,
计算$\stackrel{∧}{y}$=6.5×2018-12817.8=299.2≈300(万件),
故可预测2018年的商品需求量为300万件.
点评 本题考查了线性回归方程的求法与应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x年 | 3 | 5 | 6 | 7 | 9 |
| 年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| B. | 在线性回归分析中,回归直线不一定过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 | |
| D. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
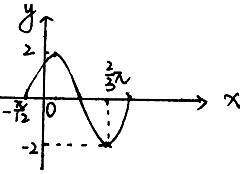 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),如图所示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com