
分析 (1)因为直线3x-4y+3=0与圆M相切,圆心(0,2)到直线的距离为r,即可求圆M的方程;
(2)①|AM|2=|MP||MQ|,所以|MQ|=3,求出Q的坐标,即可求出直线MQ的方程;
②求出直线AB的方程,即可证明直线AB恒过定点.
解答 解:(1)因为直线3x-4y+3=0与圆M相切,
故圆心(0,2)到直线的距离为r,即:$\frac{{|{-8+3}|}}{5}=r$,r=1.
所以圆的方程为x2+(y-2)2=1.
(2)①设直线MQ,AB交于点P,则$|{AP}|=\frac{{2\sqrt{2}}}{3}$,
又|AM|=1,所以$|{MP}|=\sqrt{1-{{({\frac{{2\sqrt{2}}}{3}})}^2}}=\frac{1}{3}$,
而|AM|2=|MP||MQ|,所以|MQ|=3,
设Q(x0,0),而点M(0,2),由$\sqrt{{x_0}^2+{2^2}}=3$,${x_0}=±\sqrt{5}$,
则$Q({\sqrt{5},0})$或$Q({-\sqrt{5},0})$,
从而直线MQ的方程为:$2x+\sqrt{5}y-2\sqrt{5}=0$或$2x-\sqrt{5}y+2\sqrt{5}=0$.
②证明:设点Q(q,0),由几何性质可以知道,A,B在以MQ为直径的圆上,
此圆的方程为x2+y2-qx-2y=0,AB为两圆的公共弦,
两圆方程相减得qx-2y+3=0,
即$AB:y=\frac{q}{2}x+\frac{3}{2}$,
所以过定点$({0,\frac{3}{2}})$.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,体现了数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
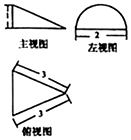
| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}π$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ac>bc,则a>b | B. | 若a>b,c>d,则ac>bd | ||
| C. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | D. | 若ac2>bc2,则a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
| 需要量(万件) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com