练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．下面几种推理是合情推理的是（　　）
    ①由圆的性质类比出球的有关性质
    ②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°
    ③某次考试张军成绩是100分，由此推出全班同学成绩都是100分
    ④数列1，0，1，0，…，推测出每项公式an=$\frac{1}{2}$+（-1）n+1•$\frac{1}{2}$．
    A．①②B．①③④C．①②④D．②④

    分析 合情推理分为归纳推理与类比推理，对①、②、③、④的推理过程逐个分析，即可得到答案．

    解答 解：合情推理分为归纳推理与类比推理，
    对于①，由圆的性质类比出球的有关性质，推理过程由圆的性质类比出球的有关性质，是类比推理，故①为合情推理；
    对于②，由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°，符合归纳推理的定义，为归纳推理，故②为合情推理；
    对于③，某次考试张军成绩是100分，由此推出全班同学成绩都是100分，是由特殊到特殊的推理过程，故③不是合情推理；
    对于④，数列1，0，1，0，…，推测出每项公式an=$\frac{1}{2}$+（-1）n+1•$\frac{1}{2}$，是由特殊到一般的推理过程，为归纳推理，故④是合情推理；
    综上所述，①②④的推理是合情推理，
    故选：C．

    点评 本题考查命题的真假判断与应用，突出考查合情推理及其分类：归纳推理与类比推理的应用，判断一个推理过程是否是归纳推理关键是看他是否符合归纳推理的定义，即是否是由特殊到一般的推理过程，判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义，即是否是由特殊到与它类似的另一个特殊的推理过程；掌握概念是正确判断的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=$\left\{\begin{array}{l}{a，x=1}\\{（\frac{1}{2}）^{|x-1|}+1，x≠1}\end{array}\right.$，若方程2f2（x）-（2a+3）f（x）+3a=0有5个不同的实数解，则a的范围是（　　）
    A．（1，$\frac{3}{2}$）∪（$\frac{3}{2}$，2）B．（1，2）∪（2，3）C．（1，+∞）D．（1，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．执行如图所示的程序框图，若输出的n=4，则输入整数p的最大值是（　　）
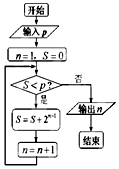
    A．4B．7C．8D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知等差数列{an}中，a5=9，a7=13，等比数列{bn}的通项公式bn=2n-1，n∈N*．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）求数列{an+bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设函数f（x）=$\frac{1}{3}$x3-$\frac{a}{2}$x2+bx+c，曲线y=f（x）在点（0，f（0））处的切线方程为y=1．
    （1）求b，c的值；
    （2）若a＞0，求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．一名射击运动员射击10次，命中环数如下，则该运动员命中环数的标准差为（　　）
    10  10  10  9  10  8  8  10  10  8．
    A．0.81B．0.9C．0.64D．0.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知圆M：x2+（y-2）2=r2（r＞0）与曲线C：（y-2）（3x-4y+3）=0有三个不同的交点．
    （1）求圆M的方程；
    （2）已知点Q是x轴上的动点，QA，QB分别切圆M于A，B两点．
    ①若$|{AB}|=\frac{{4\sqrt{2}}}{3}$，求|MQ|及直线MQ的方程；
    ②求证：直线AB恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数y=|sin2x-4sinx-a|的最大值为4，则常数a=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知f（x+y）=f（x）-f（y）对全体实数x，y都成立，则f（x）是（　　）
    A．奇函数B．偶函数
    C．既是奇函数又是偶函数D．非奇非偶函数

    查看答案和解析>>

    同步练习册答案