
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
分析 根据题意,用特殊值法分析:在f(x+y)=f(x)-f(y)中,令x=y=0可得f(0)=0,再令y=-x可得:f[x+(-x)]=f(x)+f(-x),即f(0)=f(x)+f(-x),由f(0)的值,可得f(-x)=-f(x),由偶函数的性质即可得答案.
解答 解:根据题意,f(x+y)=f(x)-f(y)对全体实数x,y都成立,
令x=y=0可得:f(0+0)=f(0)-f(0)=0,即f(0)=0,
再令y=-x可得:f[x+(-x)]=f(x)+f(-x),即f(0)=f(x)+f(-x),
又由f(0)=0,则有f(x)+f(-x)=0,即f(-x)=-f(x),
则函数f(x)为偶函数;
故选:B.
点评 本题考查函数奇偶性的判定,涉及抽象函数的问题,一般利用特殊值法分析.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
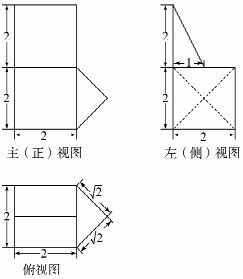
| A. | $\frac{40}{3}$ | B. | $\frac{34}{3}$ | C. | $10+\frac{{4\sqrt{2}}}{3}$ | D. | $6+\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都不大于-2 | B. | 都不小于-2 | ||
| C. | 至少有一个不大于-2 | D. | 至少有一个不小于-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com