
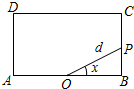
 »γΆΦΘ§“―÷ΣΨΊ–ΈABCD÷–Θ§AB=2Θ§BC=1Θ§OΈΣœΏΕΈABΒΡ÷–ΒψΘ§Ε·ΒψP¥”B≥ωΖΔΘ§―ΊΨΊ–ΈABCDΒΡ±ΏΡφ ±’κ‘ΥΕ·Θ§‘ΥΕ·÷ΝAΒψ ±÷’÷ΙΘ°…ηΓœBOP=xΘ§OP=dΘ§ΫΪd±μ ΨΈΣxΒΡΚ· ΐd=fΘ®xΘ©Θ°‘ρœ¬Ν–ΟϋΧβ÷–ΘΚ
»γΆΦΘ§“―÷ΣΨΊ–ΈABCD÷–Θ§AB=2Θ§BC=1Θ§OΈΣœΏΕΈABΒΡ÷–ΒψΘ§Ε·ΒψP¥”B≥ωΖΔΘ§―ΊΨΊ–ΈABCDΒΡ±ΏΡφ ±’κ‘ΥΕ·Θ§‘ΥΕ·÷ΝAΒψ ±÷’÷ΙΘ°…ηΓœBOP=xΘ§OP=dΘ§ΫΪd±μ ΨΈΣxΒΡΚ· ΐd=fΘ®xΘ©Θ°‘ρœ¬Ν–ΟϋΧβ÷–ΘΚ| AΘ° | ΔΌΔΎ | BΘ° | ΔΎΔέ | CΘ° | ΔΌΔΎΔή | DΘ° | ΔΌΔΎΔέΔή |
Ζ÷Έω Ω…»Γ±ΏCDΒΡ÷–ΒψΈΣEΘ§’β―υΗυΨίΚ· ΐΒΞΒς–‘ΒΡΕ®“εΦΑΆΦ–Έ÷–xΘ§dΒΡ±δΜ·ΙΊœΒ±ψΩ…≈–Εœ≥ωΚ· ΐd=fΘ®xΘ©”–4ΗωΒΞΒς«χΦδΘ§≤ΔΩ…«σ≥ωΗΟΚ· ΐΒΡΦΪ÷ΒΒψΗω ΐΘ§“‘ΦΑfΘ®xΘ©ΒΡΉν¥σΓΔΉν–Γ÷ΒΘ§¥”Εχ≈–Εœ≥ωΟΩΗωΟϋΧβΒΡ’ΐΈσΘ§¥”Εχ’“≥ω’ΐ»Ζ―ΓœνΘ°
Ϋβ¥π ΫβΘΚΗυΨίΆΦ–ΈΘ§P‘ΎBC…œ ±Θ§ΥφΉ≈xΒΡ‘ω¥σΘ§d≤ΜΕœ‘ω¥σΘ§Γύ¥Υ ±d=fΘ®xΘ©Βί‘ωΘΜ
»τ»ΓœΏΕΈCDΒΡ÷–ΒψEΘ§Ά§άμΒΟΘ§P¥”CΒΫE ±Θ§d=fΘ®xΘ©ΒίΦθΘ§P¥”ΕχEΒΫD ±Θ§d=fΘ®xΘ©Βί‘ωΘ§P¥”DΒΫA ±Θ§d=fΘ®xΘ©ΒίΦθΘΜ
ΓύΚ· ΐd=fΘ®xΘ©”–4ΗωΒΞΒς«χΦδΘ§”–»ΐΗωΦΪ÷ΒΒψΘΜ
«“d=fΘ®xΘ©ΒΡΉν–Γ÷ΒΈΣ1Θ§Ήν¥σ÷Β$\sqrt{2}$ΘΜ
ΓύΥΡΗωΟϋΧβ»Ϊ’ΐ»ΖΘ°
Ι ―ΓDΘ°
ΒψΤά ΩΦ≤ιΚ· ΐΒΞΒς–‘ΒΡΕ®“εΘ§Ιέ≤λΆΦ–ΈΒΡΡήΝΠΘ§“‘ΦΑΚ· ΐΒΡΦΪ÷ΒΒψΒΡΕ®“εΦΑ«σΖ®Θ§Κ· ΐΉν¥σΓΔΉν–Γ÷ΒΒΡΗ≈ΡνΦΑ«σΖ®Θ°


 ΒΎ1ΨμΒΞ‘Σ‘¬ΩΦΤΎ÷–ΤΎΡ©œΒΝ–¥πΑΗ
ΒΎ1ΨμΒΞ‘Σ‘¬ΩΦΤΎ÷–ΤΎΡ©œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 3Π– | BΘ° | 4Π– | CΘ° | Θ®3+2$\sqrt{2}$Θ©Π– | DΘ° | Θ®3+$\sqrt{3}$Θ©Π– |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ≥δΖ÷≤Μ±Ί“ΣΧθΦΰ | BΘ° | ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ | ||
| CΘ° | ≥δ“ΣΧθΦΰ | DΘ° | Φ»≤Μ≥δΖ÷”÷≤Μ±Ί“ΣΧθΦΰ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
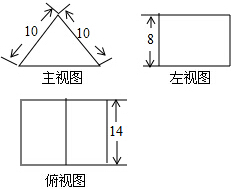
| AΘ° | 672 | BΘ° | 1120 | CΘ° | 1344 | DΘ° | 2016 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1ΓΪPΘ®XΘΦ1Θ© | BΘ° | $\frac{1-2PΘ®XΘΦ1Θ©}{2}$ | CΘ° | PΘ®0ΘΦXΘΦ1Θ© | DΘ° | $\frac{1+2PΘ®XΘΦ1Θ©}{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
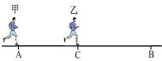 »γΆΦΥυ ΨΘ§ΦΉ¥”AΒΊ”…Ψ≤÷Ι‘»Φ”ΥΌ≈ήœρBΒΊΘ§Β±ΦΉ«ΑΫχΨύάκΈΣx1 ±Θ§““¥”ΨύAΒΊx2¥ΠΒΡCΒψ”…Ψ≤÷Ι≥ωΖΔΘ§Φ”ΥΌΕ»”κΦΉœύΆ§Θ§ΉνΚσΕΰ»ΥΆ§ ±ΒΫ¥οBΒΊΘ§‘ρABΝΫΒΊΨύάκΈΣΘ®ΓΓΓΓΘ©
»γΆΦΥυ ΨΘ§ΦΉ¥”AΒΊ”…Ψ≤÷Ι‘»Φ”ΥΌ≈ήœρBΒΊΘ§Β±ΦΉ«ΑΫχΨύάκΈΣx1 ±Θ§““¥”ΨύAΒΊx2¥ΠΒΡCΒψ”…Ψ≤÷Ι≥ωΖΔΘ§Φ”ΥΌΕ»”κΦΉœύΆ§Θ§ΉνΚσΕΰ»ΥΆ§ ±ΒΫ¥οBΒΊΘ§‘ρABΝΫΒΊΨύάκΈΣΘ®ΓΓΓΓΘ©| AΘ° | x1+x2 | BΘ° | $\frac{Θ®{x}_{1}+{x}_{2}Θ©^{2}}{4{x}_{1}}$ | ||
| CΘ° | $\frac{{x}_{1}^{2}}{4Θ®{x}_{1}+{x}_{2}Θ©}$ | DΘ° | $\frac{Θ®{x}_{1}+{x}_{2}Θ©^{2}}{Θ®{x}_{1}-{x}_{2}Θ©{x}_{1}}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com