17.利用定积分的定义计算${∫}_{2}^{3}$(x+2)dx.
分析 利用定积分的计算公式解答.
解答 解:(1)分割
如图,把曲边梯形ABCD分割成n个小曲边梯形,用分点
.
,…
把区间[1,2]等分成n个小区间,每个小区间的长度为△x=
,过各分点作x轴的垂线,把曲边梯形ABCD分割成n个小曲边梯形,它们的面积分别记作△S
1,△S
2,…,△S
n.
(2)近似代替取各小区间的左端点ξ
i,用以点ξ
i的纵坐标ξ
i3为一边,以小区间长△x=
为其邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为
△S
i≈ξ
i3•△x=(
)3•
(i=1,2,3,…,n).
(3)求和
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值,即S=
| n |
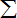 |
| i=1 |
△Si=
| n |
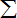 |
| i=1 |
(
)3•
①
(4)求极限
当分点数目愈多,即△x愈小时,和式①的值就愈接近曲边梯形ABCD的面积S.因此,n→∞即△x→0时,和式①的极限就是所求的曲边梯形ABCD的面积.
| n |
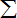 |
| i=1 |
(
)3•
=
•
| n |
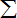 |
| i=1 |
(n+i-1)
3=
•[n(n-1)
3+3(n-1)
2•
+3(n-1)•
(n+1)(2n+1)+
n2(n+1)2,
∴S=
| n |
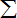 |
| i=1 |
(
)3•
=1+
+1+
=
.解:${∫}_{2}^{3}$(x+2)dx=($\frac{1}{2}{x}^{2}+2x$)|${\;}_{2}^{3}$=$\frac{9}{2}$;
点评 本题考查了定积分的计算;关键是熟记公式.

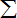


 在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是AB、B1C1的中点.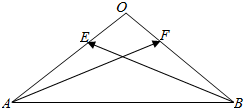 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.