
分析 (1)由题意可得,所有的(x,y)共计有6×6=36个,其中满足-2x+y=-1,其中满足2x-y=1的有3个,从而求得满足-2x+y=-1的概率.
(2)如图,则所有的(x,y)构成边长为5正方形区域,满足-2x+y<0的(x,y)构成的区域为梯形,即图中阴影部分,从而求得满足-2x+y<0的概率为 $\frac{{S}_{梯形}}{{S}_{正方形}}$ 的值.
解答 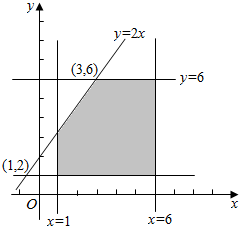 解:(1)由题意可得,所有的(x,y)共计有6×6=36个,其中满足-2x+y=-1,
解:(1)由题意可得,所有的(x,y)共计有6×6=36个,其中满足-2x+y=-1,
即满足2x-y=1的有(1,1)、(2,3)、(3,5),共计3个,
故满足-2x+y=-1的概率为$\frac{3}{36}$=$\frac{1}{12}$.
(2)若x,y在区间[1,6]上取值,则所有的(x,y)构成边长为5正方形区域,
满足-2x+y<0的(x,y)构成的区域为梯形,即图中阴影部分,
故满足-2x+y<0的概率为 $\frac{{S}_{梯形}}{{S}_{正方形}}$=$\frac{25-\frac{1}{2}×2×4}{25}$=$\frac{21}{25}$.
点评 本题主要考查古典概率和几何概型,体现了数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A、B、C为函数y=log2x图象上的三点,它们的横坐标为t,t+2,t+4,(其中t≥1),AA1、BB1、CC1与x轴垂直,垂足为A1、B1、C1.
如图,A、B、C为函数y=log2x图象上的三点,它们的横坐标为t,t+2,t+4,(其中t≥1),AA1、BB1、CC1与x轴垂直,垂足为A1、B1、C1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | ($\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,$\frac{5}{4}$) | D. | [1,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$ | B. | $\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$ | C. | $\frac{3}{5}\overrightarrow{a}+\frac{4}{5}\overrightarrow{b}$ | D. | $\frac{4}{5}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
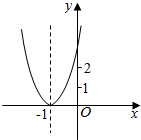 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com