
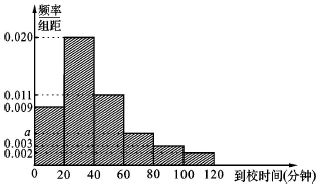
 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:分析 (1)由频率和为1,列方程求出a的值,再计算平均到校时间;
(2)计算不住校人数的频率值,求出此时对应的到校时间即可.
解答 解:(1)由频率和为1,得
(0.009+0.020+0.011+a+0.003+0.002)×20=1,
解得a=0.005;
所以平均到校时间为
$\overline x=({10×0.009+30×0.020+50×0.011+70×0.005+90×0.003+110×0.002})×20=41.6$(分钟)
(2)住校人数占总数60%,则不住校人数占总数40%,
列式计算:x0=40-${x_0}=40-\frac{0.009×20+0.020×20-0.4}{0.020×20}×20=31$(分钟),
所以从家到校时间为31分钟以上开始住校.
点评 本题考查了频率分布直方图的应用问题,是基础题目.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
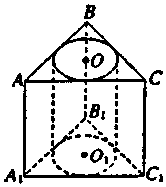 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
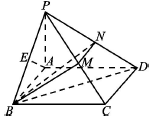 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
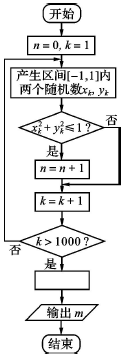
| A. | $m=1-\frac{n}{1000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=1-\frac{n}{250}$ | D. | $m=\frac{n}{250}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com