练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    分析 利用直线与直线的平行条件得出k1=k2，结合充分必要条件判断即可．

    解答 解：若“a=3”成立，则两直线的方程分别是3x-2y-1=0与6x-4y+1=0，k1=k2=$\frac{3}{2}$．
    所以两直线一定平行；
    反之，当“直线ax-2y-1=0与直线6x-4y+1=0平行”成立时，有$\frac{a}{6}$=$\frac{1}{2}$，所以a=3；
    所以“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的必要充分条件，
    故选：A．

    点评 本题简单的考查了直线的平行的条件，充分必要条件的概念，难度不大，属于容易题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．设Sn为等差数列{an}的前n项和，若a3=4，S9-S6=27，则S10=65．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在正方体ABCD-A1B1C1D1各条棱所在的直线中，与直线AA1垂直的条数共有8条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

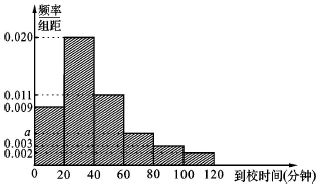    14．某校收集该校学生从家到学校的时间后，制作成如下的频率分布直方图：
    （1）求a的值及该校学生从家到校的平均时间；
    （2）若该校因学生寝室不足，只能容纳全校60%的学生住校，出于安全角度考虑，从家到校时间较长的学生才住校，请问从家到校时间多少分钟以上开始住校．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知命题甲：对任意实数x∈R，不等式$\frac{{a{x^2}-ax+3}}{{{x^2}-2x+2}}≥0$恒成立；命题乙：已知x，y∈R*满足x+y=xy+3=0，且a≤xy恒成立．
    （1）分别求出甲、乙为真命题时，实数a的取值范围；
    （2）求实数a的取值范围，使命题甲、乙中有且只有一个真命题．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

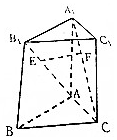    15．如图，在三棱柱ABC-A1B1C1中，已知E，F分别是线段AB1与CA1上的动点，异面直线AB1与CA1所成角为θ，记线段EF中点M的轨边为L，则|L|等于（　　）
    A．$\frac{1}{2}$|AB1|
    B．$\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-（\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}}）^{2}}$
    C．$\frac{1}{4}$|AB1|•|CA1|•sinθ
    D．$\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$（V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的体积）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在数列{an}及{bn}中，an+1=an+bn+$\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$，bn+1=an+bn-$\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$，a1=1，b1=1．设cn=$\frac{1}{{a}_{n}}+\frac{1}{{b}_{n}}$，则数列{cn}的前2017项和为4034．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．椭圆E的焦点在x轴上，中心在原点，其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点，则椭圆E的标准方程为（　　）
    A．$\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$B．$\frac{x^2}{2}+{y^2}=1$C．$\frac{x^2}{4}+\frac{y^2}{2}=1$D．$\frac{y^2}{4}+\frac{x^2}{2}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．在直角坐标系xoy中，曲线C的参数方程为$\left\{\begin{array}{l}x=acost\\ y=2sint\end{array}\right.$（t为参数，a＞0）以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，已知直线l的极坐标方程为$ρcos（{θ+\frac{π}{4}}）=-2\sqrt{2}$．
    （Ⅰ）设P是曲线C上的一个动点，当a=2时，求点P到直线l的距离的最小值；
    （Ⅱ）若曲线C上的所有点均在直线l的右下方，求a的取值范围．

    查看答案和解析>>

    同步练习册答案