
分析 由已知可得an+1+bn+1=2(an+bn),a1+b1=2,an+1bn+1=$({a}_{n}+{b}_{n})^{2}-({{a}_{n}}^{2}+{{b}_{n}}^{2})=2{a}_{n}{b}_{n}$,即anbn=2n-1.代入cn=$\frac{1}{{a}_{n}}+\frac{1}{{b}_{n}}$,求得数列{cn}为常数数列得答案.
解答 解:∵an+1=an+bn+$\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$,bn+1=an+bn-$\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$,a1=1,b1=1.
∴an+1+bn+1=2(an+bn),a1+b1=2.
∴an+bn=2n.
另一方面:an+1bn+1=$({a}_{n}+{b}_{n})^{2}-({{a}_{n}}^{2}+{{b}_{n}}^{2})=2{a}_{n}{b}_{n}$,
∴anbn=2n-1.
∴cn=$\frac{1}{{a}_{n}}+\frac{1}{{b}_{n}}$=$\frac{{a}_{n}+{b}_{n}}{{a}_{n}{b}_{n}}$=$\frac{{2}^{n}}{{2}^{n-1}}=2$,
则数列{cn}的前2017项和S2017=2017×2=4034.
故答案为:4034.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
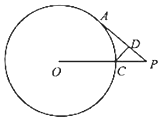 如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.
如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
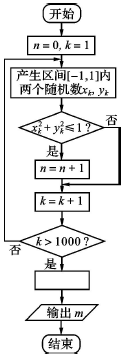
| A. | $m=1-\frac{n}{1000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=1-\frac{n}{250}$ | D. | $m=\frac{n}{250}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
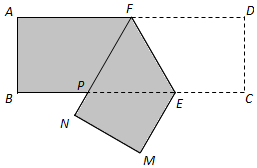 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.
如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com