
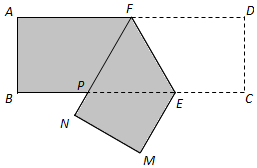
 ��ͼ��ij��е��Ҫ����6m����2m�ij�������ƤABCD���вü�����֪��FΪAD���е㣬��E�ڱ�BC�ϣ��ü�ʱ�Ƚ��ı���CDFE��ֱ��EF���۵�MNFE������C��D�ֱ�����ֱ��BC�·���M��N����FN����BC�ڵ�P��������ֱ��PE�ü���
��ͼ��ij��е��Ҫ����6m����2m�ij�������ƤABCD���вü�����֪��FΪAD���е㣬��E�ڱ�BC�ϣ��ü�ʱ�Ƚ��ı���CDFE��ֱ��EF���۵�MNFE������C��D�ֱ�����ֱ��BC�·���M��N����FN����BC�ڵ�P��������ֱ��PE�ü������� ��1������EFP=$\frac{��}{4}$ʱ���������á�EFP=��EFD=��FEP=$\frac{��}{4}$���ɵ�FN��BC���ı���MNPEΪ���Σ����ɵó���
��2���ⷨһ����$��EFD=��\;\;��0���ȣ�\frac{��}{2}��$����������֪��EFP=��EFD=��FEP=�ȣ��ɵ�$PF=\frac{2}{sin����-2�ȣ�}=\frac{2}{sin2��}$��$NP=NF-PF=3-\frac{2}{sin2��}$��$ME=3-\frac{2}{tan��}$���ı���MNPE���Ϊ$S=\frac{1}{2}��NP+ME��MN$=$\frac{1}{2}[{��3-\frac{2}{sin2��}��+��3-\frac{2}{tan��}��}]��2$=$6-\frac{2}{tan��}-\frac{2}{sin2��}$���������û�������ʽ�����ʼ��ɵó���
�ⷨ������BE=tm��3��t��6����ME=6-t���ɵ�PE=PF����$\sqrt{��3-BP{��^2}+{2^2}}=t-BP$��$BP=\frac{{13-{t^2}}}{2��3-t��}$��NP=3-T+$\frac{13-{t}^{2}}{2��3-t��}$���ı���MNPE���Ϊ$S=\frac{1}{2}��NP+ME��MN$=$\frac{1}{2}[{��3-t+\frac{{13-{t^2}}}{2��3-t��}��+��6-t��}]��2$=$6-[{\frac{3}{2}��t-3��+\frac{2}{t-3}}]$�����û�������ʽ�����ʼ��ɵó���
��� �⣺��1������EFP=$\frac{��}{4}$ʱ���������á�EFP=��EFD=��FEP=$\frac{��}{4}$��
���ԡ�FPE=$\frac{��}{2}$������FN��BC��
�ı���MNPEΪ���Σ���3��
�����ı���MNPE�����S=PN•MN=2m2����5��
��2���ⷨһ��
��$��EFD=��\;\;��0���ȣ�\frac{��}{2}��$����������֪��EFP=��EFD=��FEP=�ȣ�
����$PF=\frac{2}{sin����-2�ȣ�}=\frac{2}{sin2��}$��$NP=NF-PF=3-\frac{2}{sin2��}$��$ME=3-\frac{2}{tan��}$�� ��8��
��$\left\{\begin{array}{l}3-\frac{2}{sin2��}��0\\ 3-\frac{2}{tan��}��0\\ 0���ȣ�\frac{��}{2}\end{array}\right.$��$\left\{\begin{array}{l}sin2�ȣ�\frac{2}{3}\\ tan�ȣ�\frac{2}{3}��\;\;\;\;\;\;\;\;\;��*��\\ 0���ȣ�\frac{��}{2}.\end{array}\right.$
�����ı���MNPE���Ϊ$S=\frac{1}{2}��NP+ME��MN$=$\frac{1}{2}[{��3-\frac{2}{sin2��}��+��3-\frac{2}{tan��}��}]��2$=$6-\frac{2}{tan��}-\frac{2}{sin2��}$=$6-\frac{2}{tan��}-\frac{{2��{{sin}^2}��+{{cos}^2}�ȣ�}}{2sin��cos��}$=$6-��tan��+\frac{3}{tan��}��$��12��
$��6-2\sqrt{tan��\frac{3}{tan��}}=6-2\sqrt{3}$��
���ҽ���$tan��=\frac{3}{tan��}$����$tan��=\sqrt{3}\;����=\frac{��}{3}$ʱȡ��=������14��
��ʱ����*��������
�𣺵�$��EFD=\frac{��}{3}$ʱ����ֱ��PE�ü����ı���MNPE������
���ֵΪ$6-2\sqrt{3}$m2�� ��16��
�ⷨ����
��BE=tm��3��t��6����ME=6-t��
����EFP=��EFD=��FEP������PE=PF����$\sqrt{��3-BP{��^2}+{2^2}}=t-BP$��
����$BP=\frac{{13-{t^2}}}{2��3-t��}$��$NP=3-PF=3-PE=3-��t-BP��=3-t+\frac{{13-{t^2}}}{2��3-t��}$�� ��8��
��$\left\{\begin{array}{l}3��t��6\\ \frac{{13-{t^2}}}{2��3-t��}��0\\ 3-t+\frac{{13-{t^2}}}{2��3-t��}��0\end{array}\right.$��$\left\{\begin{array}{l}3��t��6\\ t��\sqrt{13}��\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;��*��\\{t^2}-12t+31��0.\end{array}\right.$
�����ı���MNPE���Ϊ$S=\frac{1}{2}��NP+ME��MN$=$\frac{1}{2}[{��3-t+\frac{{13-{t^2}}}{2��3-t��}��+��6-t��}]��2$=$\frac{{3{t^2}-30t+67}}{2��3-t��}$��12��
=$6-[{\frac{3}{2}��t-3��+\frac{2}{t-3}}]$$��6-2\sqrt{3}$��
���ҽ���$\frac{3}{2}��t-3��=\frac{2}{t-3}$����$t=3+\sqrt{\frac{4}{3}}\;=3+\frac{{2\sqrt{3}}}{3}$ʱȡ��=���� ��14��
��ʱ����*��������
�𣺵���E��B��$3+\frac{{2\sqrt{3}}}{3}$mʱ����ֱ��PE�ü����ı���MNPE������
���ֵΪ$6-2\sqrt{3}$m2�� ��16�֣�
���� ���⿼���˺��������ʡ����ε�������㹫ʽ����������ʽ�����ʡ����Ǻ����ĵ�����Ӧ����ֵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
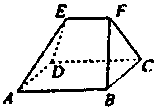 ��ͼ���ڶ�����ABCDEF�У��ı���ABCD�DZ߳�Ϊ3�������Σ�EF��AB��EF=$\frac{3}{2}$���ҵ�E��ƽ��ABCD�ľ���Ϊ2����ö���������Ϊ��������
��ͼ���ڶ�����ABCDEF�У��ı���ABCD�DZ߳�Ϊ3�������Σ�EF��AB��EF=$\frac{3}{2}$���ҵ�E��ƽ��ABCD�ľ���Ϊ2����ö���������Ϊ��������| A�� | $\frac{9}{2}$ | B�� | 5 | C�� | 6 | D�� | $\frac{15}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B�� | $\frac{x^2}{2}+{y^2}=1$ | C�� | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D�� | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʹ�������ֻ����� | ��ʹ�������ֻ����� | �ϼ� | |
| ѧϰ�ɼ��������� | 4 | 8 | 12 |
| ѧϰ�ɼ����������� | 16 | 2 | 18 |
| �ϼ� | 20 | 10 | 30 |
| P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com