
分析 利用函数图象的性质求出f(x)的解析式,根据正弦函数的单调性得出f(x)的单调减区间.
解答 解:∵f(x)的图象过点(0,$\frac{1}{2}$),∴sinφ=$\frac{1}{2}$,∵0<φ<$\frac{π}{2}$,∴φ=$\frac{π}{6}$.
∵f(x)的图象相邻两条对称轴的距离为$\frac{π}{2}$,∴T=$\frac{2π}{ω}$=π,∴ω=2.
∴f(x)=sin(2x+$\frac{π}{6}$),
令$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,解得$\frac{π}{6}$+kπ≤x≤$\frac{2π}{3}$+kπ,k∈Z.
∴函数f(x)在[0,π]上的单调递减区间为[$\frac{π}{6}$+kπ,$\frac{2π}{3}$+kπ]∩[0,π]=[$\frac{π}{6}$,$\frac{2π}{3}$].
故答案为:$[\frac{π}{6},\frac{2π}{3}]$.
点评 本题考查了正弦函数的图象与性质,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
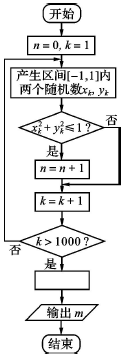
| A. | $m=1-\frac{n}{1000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=1-\frac{n}{250}$ | D. | $m=\frac{n}{250}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
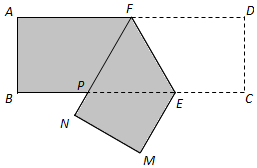 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.
如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
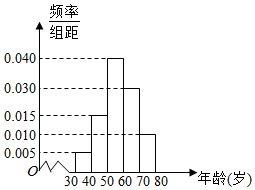 某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.
某研究小组到社区了解参加健美操运动人员的情况,用分层抽样的方法抽取了40人进行调查,按照年龄分成五个小组:[30,40],(40,50],(50,60],(60,70],(70,80],并绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | 1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com