考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)a=-1时,f(x)=
x
3-x,得f′(x)=(x+1)(x-1),从而f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)设a>0,x≥0,若f(x)>-
a恒成立,只需f(x)+
a>0即可,令g(x)=f(x)+
a=
x
3-
(a+1)x
2+ax+
a,得g′(x)=(x-a)(x-1),再分情况讨论①0<a<1时②a=1时③a>1时的a的范围,从而得出答案.
解答:
解:(1)a=-1时,f(x)=
x
3-x,
∴f′(x)=(x+1)(x-1),
令f′(x)>0,解得:x>1,x<-1,
令f′(x)<0,解得:-1<x<1,
∴f(x)在(-∞,-1),(1,+∞)递增,在(-1,1)递减;
(2)设a>0,x≥0,若f(x)>-
a恒成立,
只需f(x)+
a>0即可,
令g(x)=f(x)+
a=
x
3-
(a+1)x
2+ax+
a,
∴g′(x)=(x-a)(x-1),
①0<a<1时,g(x)在(0,a),(1,+∞)递增,在(a,1)递减,
∴g(x)
最小值=g(x)
极小值=g(1)=
-
(a+1)+a+
a>0,
解得:
<a<1,
②a=1时,g′(x)≥0,g(x)在[0,+∞)单调递增,
∴g(x)
最小值=g(0)=
a>0,
③a>1时,f(x)在(0,1),(a,+∞)递增,在(1,a)递减,
∴只需g(x)
最小值=g(x)
极小值=g(a)=
a
3-
(a+1)a
2+a
2+
a>0,
解得:1<a<4,
综合①②③得:a的取值范围是(
,4).
点评:本题考察了函数的单调性,导数的应用,渗透了数形结合思想,是一道中档题.



 阅读快车系列答案
阅读快车系列答案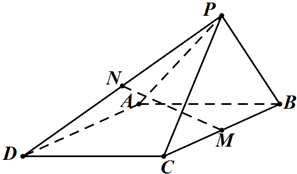 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.