【题目】已知向量
，向量
，函数
.
（1）求
的单调减区间；
（2）将函数
图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移
个单位长度，得到
的图象，求函数
的解析式及其图象的对称中心.
科目：高中数学 来源： 题型：
【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准
（吨），一位居民的月用水量不超过
的部分按平价收费，超过
的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照
， 
， 
， 
分成9组，制成了如图所示的频率分布直方图.
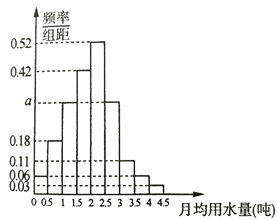
（Ⅰ）求直方图中
的值；
（Ⅱ）若将频率视为概率，从该城市居民中随机抽取3人，记这3人中月均用水量不低于3吨的人数为
，求
的分布列与数学期望.
（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准
（吨），估计
的值（精确到0.01），并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知两条直线l1（3+m）x+4y=5﹣3m，l2 2x+（5+m）y=8．当m分别为何值时，l1与l2：
（1）相交？
（2）平行？
（3）垂直？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某大学自主招生的面试中，考生要从规定的6道科学题，4道人文题共10道题中，随机抽取3道作答，每道题答对得10分，答错或不答扣5分，已知甲、乙两名考生参加面试，甲只能答对其中的6道科学题，乙答对每道题的概率都是
，每个人答题正确与否互不影响.
（1）求考生甲得分
的分布列和数学期望
；
（2）求甲，乙两人中至少有一人得分不少于15分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一周期内的图象时，列表并填入了部分数据，如下表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin（ωx+φ） | 3 | 0 |
（1）请将上表空格中的数据在答卷的相应位置上，并求函数f（x）的解析式；
（2）若y=f（x）的图象上所有点向左平移 
个单位后对应的函数为g（x），求当x∈[﹣ 
， ]时，函数y=g（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关，通过随机抽查110名学生，得到如下2×2的列联表：
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式
，算得
附表：
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表，以下结论正确是（ ）
A. 有
以上的把握认为“爱好该项运动与性别有关”
B. 有以上的把握认为“爱好该项运动与性别无关”
C. 有
以上的把握认为“爱好该项运动与性别有关”
D. 有
以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从参加某次高中英语竞赛的学生中抽出100名，将其成绩整理后，绘制频率分布直方图（如图所示）．其中样本数据分组区间为： 
， 
， 
， 
， 
， 
.
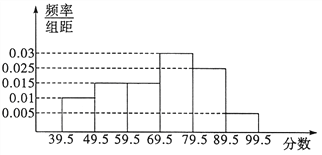
（Ⅰ）试求图中
的值，并计算区间
上的样本数据的频率和频数；
（Ⅱ）试估计这次英语竞赛成绩的众数、中位数及平均成绩（结果精确到
）.
注：同一组数据用该组区间的中点值作为代表
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将向量
=(
， 
)， 
=(
， 
)，…
=(
,
)组成的系列称为向量列{
}，并定义向量列{
}的前
项和
．如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量，那么称这样的向量列为等差向量列。若向量列{
}是等差向量列，那么下述四个向量中，与
一定平行的向量是 ( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
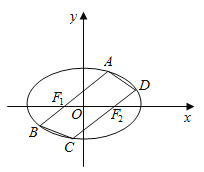
【题目】如图所示，椭圆E的中心为坐标原点，焦点
在
轴上，且
在抛物线
的准线上，点
是椭圆E上的一个动点， 
面积的最大值为
.
（Ⅰ）求椭圆E的方程；
（Ⅱ）过焦点
作两条平行直线分别交椭圆E于
四个点.
①试判断四边形
能否是菱形，并说明理由；
②求四边形
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
