
分析 (1)利用等比数列的通项公式即可得出.
(2)bn=log2a1+log2a2+…+log2an=-1-2-…-n=-$\frac{1}{2}{n}^{2}-\frac{1}{2}$n.利用12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$及其等差数列的前n项和公式即可得出.
解答 解:(1)设等比数列{an}的公比为q,∵a1+2a2=1,a${\;}_{3}^{2}$=a5-a6.
∴a1(1+2q)=1,${a}_{1}^{2}{q}^{4}$=${a}_{1}{q}^{4}-{a}_{1}{q}^{5}$,
联立解得:a1=q=$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n}$.
(2)bn=log2a1+log2a2+…+log2an=-1-2-…-n=-$\frac{n(n+1)}{2}$=-$\frac{1}{2}{n}^{2}-\frac{1}{2}$n.
∴数列的前n项和=$-\frac{1}{2}$(12+22+…+n2)-$\frac{1}{2}$(1+2+3+…+n)
=$-\frac{1}{2}$×$\frac{n(n+1)(2n+1)}{6}$-$\frac{1}{2}×\frac{n(n+1)}{2}$
=-$\frac{n(n+1)(n+2)}{6}$.
点评 本题考查了利用12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$求和、等比数列与等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
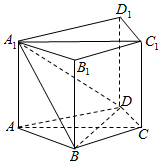 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{5π}{3}$] | B. | [-2π,-$\frac{π}{3}$] | C. | [$\frac{5π}{3}$,2π] | D. | [-2π,-$\frac{π}{3}$]和[$\frac{5π}{3}$,2π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{{\sqrt{2}π}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
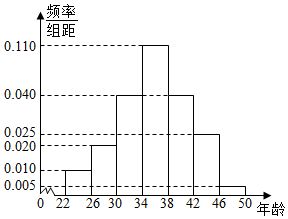 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下;
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地(已婚男性约15000人)随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 46m3 | B. | 44m3 | C. | 26m3 | D. | 25m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com