
| A. | (-∞,1) | B. | (0,1) | C. | (4e${\;}^{\frac{3}{2}}$,+∞) | D. | (0,1)∪(4e${\;}^{\frac{3}{2}}$,+∞) |
分析 判断y=ex(2x-1)的单调性,作出y=ex(2x-1)与y=a(x-1)的函数图象,根据图象交点个数和导数的几何意义得出a的范围.
解答 解:令f(x)=0得ex(2x-1)=a(x-1),
令g(x)=ex(2x-1),则g′(x)=ex(2x+1),
∴当x<-$\frac{1}{2}$时,g′(x)<0,当x>-$\frac{1}{2}$时,g′(x)>0,
∴g(x)在(-∞,-$\frac{1}{2}$)上单调递减,在(-$\frac{1}{2}$,+∞)上单调递增,
作出g(x)与y=a(x-1)的函数图象如图所示: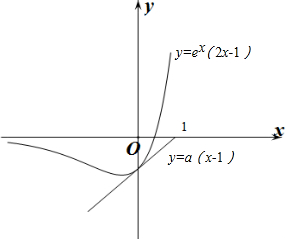
设直线y=a(x-1)与g(x)的图象相切,切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=a({x}_{0}-1)}\\{{y}_{0}={e}^{{x}_{0}}(2{x}_{0}-1)}\\{a={e}^{{x}_{0}}(2{x}_{0}+1)}\end{array}\right.$,解得x0=0,y0=-1,a=1,或x0=$\frac{3}{2}$,y0=2e${\;}^{\frac{3}{2}}$,a=4e${\;}^{\frac{3}{2}}$,
∵f(x)有两个不同的零点,
∴g(x)与y=a(x-1)的函数图象有两个交点,
∴0<a<1或a>4e${\;}^{\frac{3}{2}}$.
故选D.
点评 本题考查了函数单调性的判断,函数零点与函数图象的关系,属于中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | |||
| 学习积极性一般 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{8}{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
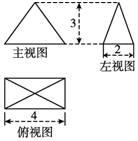
| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 2$\sqrt{10}$+$\sqrt{13}$ | D. | 4$\sqrt{10}$+2$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com