
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 利用平面向量的性质,注意分析零向量这种特殊情况,逐一判断各个选项是否正确,从而得出结论.
解答 解:由于零向量$\overrightarrow 0$方向是任意的,故$\overrightarrow 0$能与任意向量平行,故①错误;
若$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,则A.B.C.D四点共面,但不一定共线,例如当ABCD为平行四边形时,故②不正确;
在平行四边形ABCD中,一定有$\overrightarrow{AB}=\overrightarrow{DC}$,故③正确;
若$\overrightarrow m=\overrightarrow n,\;\;\overrightarrow n=\overrightarrow k$,则$\overrightarrow m=\overrightarrow k$,故④正确;
⑤若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$,则当$\overrightarrow{b}$=$\overrightarrow{0}$时,不能推出$\overrightarrow a$∥$\overrightarrow c$,故⑤错误,
故选:B.
点评 本题主要考查平面向量的性质,注意分析特殊情况,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 偶函数且最小正周期为$\frac{π}{2}$ | B. | 奇函数且最小正周期为$\frac{π}{2}$ | ||
| C. | 偶函数且最小正周期为π | D. | 奇函数且最小正周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
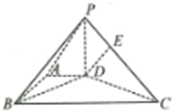 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD,AD=1,AB=$\sqrt{3}$,BC=4.
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PD⊥平面ABCD,AD=1,AB=$\sqrt{3}$,BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
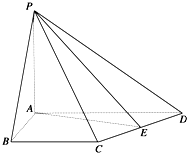 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=4,BC=3,AD=5,PA=4,∠DAB=∠ABC=90°,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=4,BC=3,AD=5,PA=4,∠DAB=∠ABC=90°,E是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2016}{2017}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com