
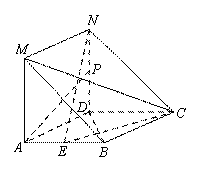
如图,在四棱锥 中,
中,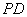 垂直于底面
垂直于底面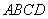 ,底面
,底面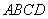 是直角梯形,
是直角梯形,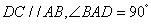 ,且
,且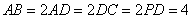 (单位:
(单位: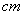 ),
),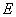 为
为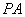 的中点。
的中点。

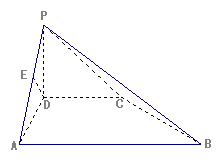 (1)如图,若正视方向与
(1)如图,若正视方向与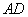 平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
(2)证明: 平面
平面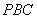 ;
;
(3)证明: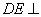 平面
平面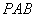 ;
;
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
2. 棱台的结构特征
| 名称 | 棱台 | 正棱台 |
| 图形 |
|
|
| 特征 | ①两底面互相平行, ②用一个平行于底面的平面去截棱锥,底面和截面之间的部分.
| 用平行于( )的底面平面截得的棱台 |
| 棱台的上下底多边形一定相似,即上底面与下底面的边长() | ||
| 面积 | 棱台侧面积 | 棱台表面积 |
| 体积 | 台体的体积 |
查看答案和解析>>
科目:高中数学 来源: 题型:
直线与平面所成的角
(1)一个平面的斜线和它在这个平面内的)______所成的角,叫做斜线和这个平面所成的角.
(2)直线与平面所成的角的范围是_________
(3)如果直线和平面垂直,那么就说直线和平面所成的角是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
在如图所示的几何体中,四边形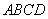 是菱形,
是菱形,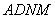 是矩形,平面
是矩形,平面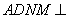 平面
平面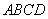 ,
,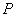 为
为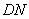 的中点.
的中点.
(1)求证: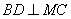 ;
;
(2)在线段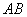 上是否存在点
上是否存在点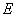 ,使得
,使得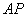 ∥平面
∥平面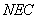 ,
,
若存在,说明其位置,并加以证明;若不存在,请说明理由.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某高速公路收费站入口处的安全标识墩如图4所示.墩的上半部分是正四棱锥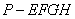 ,下半部分是长方体
,下半部分是长方体 .图5、图6分别是该标识墩的正(主)视图和俯视图.(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;(3)证明:直线
.图5、图6分别是该标识墩的正(主)视图和俯视图.(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;(3)证明:直线 平面
平面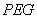 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
若命题“错误!未找到引用源。”是假命题,则实数错误!未找到引用源。的最小值为( )
A、错误!未找到引用源。 B、错误!未找到引用源。 C、错误!未找到引用源。 D、错误!未找到引用源。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数 ,
, 
(Ⅰ)若函数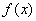 在
在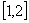 上是减函数,求实数
上是减函数,求实数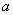 的取值范围;
的取值范围;
(Ⅱ)令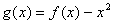 ,是否存在实数
,是否存在实数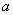 ,当
,当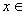
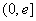 (
(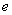 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出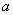 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(III)当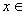
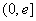 时,证明:
时,证明: 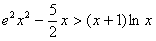
查看答案和解析>>
科目:高中数学 来源: 题型:
某市旅游部门开发一种旅 游纪念
游纪念 品,每件产品的成本是
品,每件产品的成本是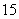 元,销售价是
元,销售价是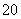 元,月平均销售
元,月平均销售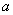 件.通过改进工艺,产品的成本不变,质量和技术
件.通过改进工艺,产品的成本不变,质量和技术 含金量提高,市场分析的结果表明,如果产
含金量提高,市场分析的结果表明,如果产 品的销售价提高的百分率为
品的销售价提高的百分率为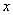
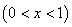 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为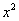 .记改进工
.记改进工 艺后,旅游部门销售该纪念品的月平均利润是
艺后,旅游部门销售该纪念品的月平均利润是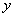 (元).
(元).
(1)写出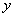 与
与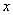 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com