
设数列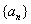 的前
的前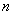 项和为
项和为 ,满足
,满足 .
.
(1)求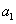 的值;
的值;
(2)求证:数列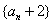 是等比数列,并求数列
是等比数列,并求数列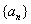 的通项公式.
的通项公式.
(3)设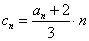 ,求数列
,求数列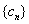 的前
的前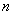 项和
项和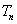
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
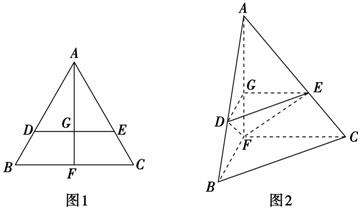
如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=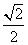 .
.
(1)证明:DE//平面BCF;(2)证明:CF⊥平面ABF;
(3)当AD=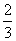 时,求三棱锥F-DEG的体积VF-DEG.
时,求三棱锥F-DEG的体积VF-DEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在四棱锥 中,
中,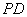 垂直于底面
垂直于底面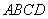 ,底面
,底面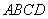 是直角梯形,
是直角梯形,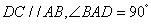 ,且
,且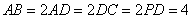 (单位:
(单位: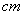 ),
),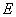 为
为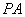 的中点。
的中点。

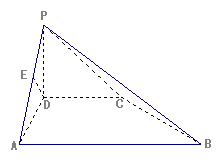 (1)如图,若正视方向与
(1)如图,若正视方向与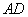 平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
(2)证明: 平面
平面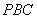 ;
;
(3)证明: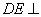 平面
平面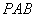 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com