
【题目】已知点M,N分别是椭圆C:![]() (
(![]() )的左顶点和上顶点,F为其右焦点,
)的左顶点和上顶点,F为其右焦点,![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设不过原点O的直线![]() 与椭圆C相交于A,B两点,若直线OA,AB,OB的斜率成等比数列,求
与椭圆C相交于A,B两点,若直线OA,AB,OB的斜率成等比数列,求![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由![]() ,结合椭圆的离心率求解即可.
,结合椭圆的离心率求解即可.
(Ⅱ)直线![]() 的斜率存在且不为0.设直线
的斜率存在且不为0.设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,联立直线和椭圆,消去
,联立直线和椭圆,消去![]() 可得,
可得,![]() ,利用判别式以及韦达定理,通过
,利用判别式以及韦达定理,通过![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,推出
的斜率依次成等比数列,推出![]() ,求出
,求出![]() ,
,![]() ,且
,且![]() ,然后求解三角形的面积的表达式,求解范围即可.
,然后求解三角形的面积的表达式,求解范围即可.
解:(Ⅰ)设椭圆的半焦距为![]() ,由题可知
,由题可知![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,则
,则![]() ,
,
又![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,
所以椭圆C的方程![]()
(Ⅱ)由题意可知,直线l的斜率存在且不为0.
故可设直线![]() ,
,![]() ,
,![]() ,
,
联立直线和椭圆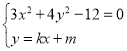 ,消去y可得,
,消去y可得,![]() ,
,
有题意可知,![]() ,
,
即![]() ,
,
且![]() ,
,![]() ,
,
又直线OA,AB,OB的斜率依次成等比数列,所以![]() ,
,
将![]() ,
,![]() 代入并整理得
代入并整理得![]() ,
,
因为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
设d为点O到直线l的距离,则有![]() ,
,
![]() ,
,
所以![]() ,
,
所以![]() 面积的取值范围为
面积的取值范围为![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() .
.
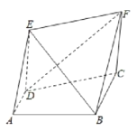
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会后我国举办的规模最大的国际体育盛会.经过激烈角逐,奖牌榜的前6名依次为中国俄罗斯巴西法国波兰和德国.其中德国队共有45名运动员获得了奖牌,其中金牌10枚银牌15枚铜牌20枚,某大学德语系同学利用分层抽样的方式从德国队获奖选手中抽取9名获奖代表.
(1)请问这9名获奖代表中获金牌银牌铜牌的人数分别为多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解城市道路交通压力,促进城市道路交通有序运转,减少机动车尾气排放对空气质量的影响,西安市人民政府决定:自2019年3月18日至2020年3月13日在相关区域实施工作日机动车尾号限行交通管理措施.已知每辆机动车每周一到周五都要限行一天,周末(周六和周日)不限行.某公司有A,B,C,D,E五辆车,每天至少有四辆车可以上路行驶.已知E车周四限行,B车昨天限行,从今天算起,A,C 两辆车连续四天都能上路行驶,E车明天可以上路,由此可知下列推测一定正确的是( )
A.今天是周四B.今天是周六C.A车周三限行D.C车周五限行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
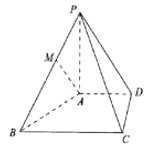
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线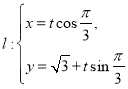 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com