
分析 (I)令f′(x)>0解出x的范围即为f(x)的单调增区间;
(II)讨论极值点与区间的关系判断f(x)在[$\frac{1}{2}$,1]上的单调性,从而求出f(x)在[$\frac{1}{2}$,1]上的最小值;
(III)利用斜率公式求出kAB,根据导数的几何意义求出曲线C在N处的切线斜率k,假设kAB=k,令$\frac{{x}_{1}}{{x}_{2}}$=t,构造函数g(t)=kAB-k,判断g(t)的单调性及零点得出结论.
解答 解:(I)f(x)的定义域为(0,+∞),
f′(x)=2ax+1-2a-$\frac{1}{x}$=$\frac{2a{x}^{2}+(1-2a)x-1}{x}$=$\frac{(2ax+1)(x-1)}{x}$.
∵a>0,x>0,∴2ax+1>0,
令f′(x)>0得x-1>0,
∴f(x)单调递增区间为(1,+∞).
(II)当a<0时,令f′(x)=0得x1=1,x2=-$\frac{1}{2a}$.
①当-$\frac{1}{2a}$≥1即-$\frac{1}{2}$≤a<0时,f(x)在(0,1)上是减函数,
∴f(x)在[$\frac{1}{2}$,1]上的最小值为f(1)=1-a.
②当$\frac{1}{2}<\frac{1}{2a}<1$即-1$<a<-\frac{1}{2}$时,f(x)在区间[$\frac{1}{2}$,-$\frac{1}{2a}$]上单调递减,在区间[-$\frac{1}{2a}$,1]上单调递增,
∴f(x)在区间[$\frac{1}{2}$,1]上的最小值为f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
③当-$\frac{1}{2a}$$≤\frac{1}{2}$即a≤-1时,f(x)在区间[$\frac{1}{2}$,1]上是增函数,
∴f(x)在区间[$\frac{1}{2}$,1]上的最小值为f($\frac{1}{2}$)=$\frac{1}{2}$-$\frac{3}{4}a+ln2$.
综上,fmin(x)=$\left\{\begin{array}{l}{\frac{1}{2}-\frac{3}{4}a+ln2,a≤-1}\\{1-\frac{1}{4a}+ln(-2a),-1<a<-\frac{1}{2}}\\{1-a,-\frac{1}{2}≤a<0}\end{array}\right.$.
(III)设M(x0,y0),则xN=x0=$\frac{{x}_{1}+{x}_{2}}{2}$.
直线AB的斜率k1=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{1}{{x}_{2}-{x}_{1}}$[a(x22-x12)+(1-2a)(x2-x1)+ln1-lnx2]=a(x1+x2)+(1-2a)+$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{2}-{x}_{1}}$.
曲线C在N处的切线斜率为k2=f′(x0)=2ax0+1-2a-$\frac{1}{{x}_{0}}$=a(x1+x2)+1-2a-$\frac{2}{{x}_{1}+{x}_{2}}$.
假设曲线C在N处的切线平行于直线AB,则k1=k2,
∴$\frac{ln{x}_{1}-ln{x}_{2}}{{x}_{2}-{x}_{1}}$=-$\frac{2}{{x}_{1}+{x}_{2}}$,
∴ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$,
令$\frac{{x}_{1}}{{x}_{2}}$=t,则lnt=$\frac{2(t-1)}{t+1}$,不妨设x1<x2,则0<t<1.
令g(t)=lnt-$\frac{2(t-1)}{t+1}$,则g′(t)=$\frac{1}{t}$-$\frac{4}{(1+t)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴g(t)在(0,1)上为增函数,
∴g(t)<g(1)=0,即g(t)=0在(0,1)上无解,
∴曲线C在N处的切线不平行于直线AB.
点评 本题考查了导数与函数单调性,函数最值的关系,导数的几何意义,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7+2\sqrt{2}}$ | B. | $\sqrt{14}$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
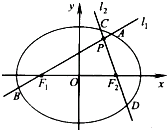 如图,分别过椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)左右焦点F1,F2的两条不同动直线l1,l2相交于P点,l1,l2与椭圆E分别交于A,B与C,D不同四点,直线OA,OB,OC,OD的斜率k1,k2,k3,k4满足k1+k2=k3+k4,已知当l1与x轴重合时,|AB|=4,|CD|=3.
如图,分别过椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)左右焦点F1,F2的两条不同动直线l1,l2相交于P点,l1,l2与椭圆E分别交于A,B与C,D不同四点,直线OA,OB,OC,OD的斜率k1,k2,k3,k4满足k1+k2=k3+k4,已知当l1与x轴重合时,|AB|=4,|CD|=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com