
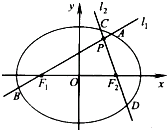
 Èçͼ£¬·Ö±đ¹ưÍÖÔ²E£º$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1£¨a£¾b£¾0£©×óÓ̉½¹µăF1£¬F2µÄÁ½̀ơ²»Í¬¶¯Ö±Ïßl1£¬l2ÏཻÓÚPµă£¬l1£¬l2ÓëÍÖÔ²E·Ö±đ½»ÓÚA£¬BÓëC£¬D²»Í¬ËÄµă£¬Ö±ÏßOA£¬OB£¬OC£¬ODµÄбÂÊk1£¬k2£¬k3£¬k4Âú×ăk1+k2=k3+k4£¬̉ÑÖªµ±l1ÓëxÖáÖغÏʱ£¬|AB|=4£¬|CD|=3£®
Èçͼ£¬·Ö±đ¹ưÍÖÔ²E£º$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1£¨a£¾b£¾0£©×óÓ̉½¹µăF1£¬F2µÄÁ½̀ơ²»Í¬¶¯Ö±Ïßl1£¬l2ÏཻÓÚPµă£¬l1£¬l2ÓëÍÖÔ²E·Ö±đ½»ÓÚA£¬BÓëC£¬D²»Í¬ËÄµă£¬Ö±ÏßOA£¬OB£¬OC£¬ODµÄбÂÊk1£¬k2£¬k3£¬k4Âú×ăk1+k2=k3+k4£¬̉ÑÖªµ±l1ÓëxÖáÖغÏʱ£¬|AB|=4£¬|CD|=3£®·ÖÎö £¨1£©µ±l1ÓëxÖáÖغÏʱ£¬CD¡ÍxÖᣬÓÉ´ËÁĐ³ö·½³̀×éÇó³öa£¬b£¬´Ó¶øÄÜÇó³öÍÖÔ²EµÄ·½³̀£®
£¨2£©µ±l1ÓëxÖáÖغÏʱ£¬l2¡ÍxÖᣬPµă¼´F2£¨1£¬0£©£¬µ±l2ÓëxÖáÖغÏʱ£¬l1¡ÍxÖᣬPµă¼´F1£¨-1£¬0£©£¬µ±l1£¬l2²»ÓëxÖáÖغÏʱ£¬ÉèP£¨x0£¬y0£©£¨x0¡Ù¡À1£¬y0¡Ù0£©£¬Éèl1£ºy=m£¨x+1£©£¬l2£ºy=n£¨x-1£©£¬ÍÖÔ²E£º$\frac{x^2}{4}+\frac{y^2}{3}=1$£¬·Ö±đ½«Ö±Ïßl1£¬l2ÓëÍÖÔ²ÁªÁ¢£¬ÔÙÀûÓĂΤ´ï¶¨Àí¡¢Ö±Ïß·½³̀£¬½áºÏ̉ÑÖª̀ơ¼₫ÄÜÇó³ö´æÔÚ¶¨µăM¡¢NΪÍÖÔ²½¹µă$£¨{0£¬¡À\sqrt{2}}£©$£¬Ê¹µĂ|PM|+|PN|Ϊ¶¨ÖµÎª¶¨Öµ£®
½â´đ ½â£º£¨¢ñ£©µ±l1ÓëxÖáÖغÏʱ£¬k1=k2=0£¬
¡àk3+k4=0£¬¡àCD¡ÍxÖᣬ
|AB|=2a=4£¬|CD|=$\frac{2{b}^{2}}{a}=3$£¬
¡à$\left\{\begin{array}{l}{2a=4}\\{\frac{2{b}^{2}}{a}=3}\end{array}\right.$£¬½âµĂa=2£¬b=$\sqrt{3}$£¬
¡àÍÖÔ²EµÄ·½³̀Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$£®¡£¨5·Ö£©
£¨¢̣£©µ±l1ÓëxÖáÖغÏʱ£¬l2¡ÍxÖᣬPµă¼´F2£¨1£¬0£©£¬
µ±l2ÓëxÖáÖغÏʱ£¬l1¡ÍxÖᣬPµă¼´F1£¨-1£¬0£©£¬
µ±l1£¬l2²»ÓëxÖáÖغÏʱ£¬ÉèP£¨x0£¬y0£©£¨x0¡Ù¡À1£¬y0¡Ù0£©£¬
Éèl1£¬l2бÂÊ·Ö±đΪm£¬n£¨m¡Ùn£¬m¡Ù0£¬n¡Ù0£©£¬
Ộ£ºl1£ºy=m£¨x+1£©£¬¢Ù£¬l2£ºy=n£¨x-1£©£¬¢Ú£¬
ÓÖÍÖÔ²E£º$\frac{x^2}{4}+\frac{y^2}{3}=1$£¬¢Û
ÉèA£¨x1£¬y1£©£¬B£¨x2£¬y2£©£¬C£¨x3£¬y3£©£¬D£¨x4£¬y4£©
ÓÉ¢Ù¢ÛÁªÁ¢µĂ£¨3+4m2£©x2+8m2x+4m2-12=0£¬
${x_1}+{x_2}=\frac{{-8{m^2}}}{{3+4{m^2}}}£¬{x_1}{x_2}=\frac{{4{m^2}-12}}{{3+4{m^2}}}$£¬¢Ü¡£¨6·Ö£©
ÓÉ ¢Ú¢ÛÁªÁ¢µĂ£¨3+4n2£©x2-8n2x+4n2-12=0£¬
${x_1}+{x_2}=\frac{{8{n^2}}}{{3+4{n^2}}}£¬{x_1}{x_2}=\frac{{4{n^2}-12}}{{3+4{n^2}}}$£¬¢Ư¡£¨7·Ö£©
ÓÉk1+k2=k3+k4£¬µĂ$\frac{y_1}{x_1}+\frac{y_2}{x_2}=\frac{y_3}{x_3}+\frac{y_4}{x_4}$£¬
ÓÖ£ºy1=m£¨x1+1£©£¬y2=m£¨x2+1£©£¬y3=n£¨x3-1£©£¬y4=n£¨x4-1£©£¬
´úÈëÉÏʽ£¬µĂ£º$m£¨{2+\frac{{{x_1}+{x_2}}}{{{x_1}{x_2}}}}£©=n£¨{2-\frac{{{x_3}+{x_4}}}{{{x_3}{x_4}}}}£©$£¬¡£¨8·Ö£©
½«¢Ü¢Ư´úÈ뻯¼̣µĂ£¨mn+3£©£¨m-n£©=0£¬¡ßm¡Ùn£¬¡àmn=-3£¬¡£¨9·Ö£©
¼´£º$\frac{y_0}{{{x_0}+1}}•\frac{y_0}{{{x_0}-1}}=-3£¨{x_0}¡Ù¡À1£©$£¬»¯¼̣µĂ£º${x_0}^2+\frac{{{y_0}^2}}{3}=1£¨{{x_0}¡Ù¡À1}£©$¡£¨10·Ö£©
ÓÉP£¨¡À1£¬0£©Âú×ăÉÏʽ£¬Ëù̉ÔPµă¹́¼£·½³̀Ϊ£º${x^2}+\frac{y^2}{3}=1$¡£¨11·Ö£©Ê¹µĂ|PM|+|PN|Ϊ¶¨Öµ
¹Ê´æÔÚ¶¨µăM£¨0£¬-$\sqrt{2}$£©¡¢N£¨0£¬$\sqrt{2}$£©ÎªÍÖÔ²½¹µă$£¨{0£¬¡À\sqrt{2}}£©$£¬Ê¹µĂ|PM|+|PN|=2$\sqrt{3}$Ϊ¶¨Öµ¡£¨12·Ö£©
µăÆÀ ±¾̀⿼²éÍÖÔ²·½³̀µÄÇ󷨣¬¿¼²éÂú×ằơ¼₫µÄµăÊÇ·ñ´æÔÚµÄÅжÏÓëÇ󷨣¬ÊÇÖеµ̀⣬½ầâʱ̉ªÈÏƠæÉó̀⣬ע̉âÍÖÔ²ĐÔÖÊ¡¢Ö±Ïß·½³̀¡¢Î¤´ï¶¨ÀíµÄºÏÀíÔËÓĂ£®


 Đ¡Ñ§¿Îʱ×÷̉µÈ«Í¨Á·°¸ÏµÁĐ´đ°¸
Đ¡Ñ§¿Îʱ×÷̉µÈ«Í¨Á·°¸ÏµÁĐ´đ°¸ ½đ°æ¿Î̀Ă¿ÎʱѵÁ·ÏµÁĐ´đ°¸
½đ°æ¿Î̀Ă¿ÎʱѵÁ·ÏµÁĐ´đ°¸ µ¥ÔªÈ«ÄÜÁ·¿¼¾íϵÁĐ´đ°¸
µ¥ÔªÈ«ÄÜÁ·¿¼¾íϵÁĐ´đ°¸ Đ»ƸԱø·¨ĂܾíϵÁĐ´đ°¸
Đ»ƸԱø·¨ĂܾíϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | £¨-1£¬-$\frac{1}{2}}$£© | B£® | £¨-$\frac{1}{2}$£¬0£© | C£® | £¨$\frac{1}{2}$£¬1£© | D£® | £¨1£¬2£© |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com