练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．在四面体ABCD中，已知AB=CD=$\sqrt{13}$，BC=DA=$\sqrt{0}$，AC=BD=$\sqrt{5}$，E，F分别是棱AC，BD的中点，则EF的长为（　　）
    A．3B．$\sqrt{3}$C．$\sqrt{2}$D．1

    分析 由题意构造出图形，然后列方程组求解．

    解答 解：如图，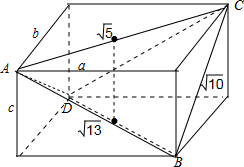

    作过一个顶点的三条棱长分别为a，b，c的长方体，使其侧面对角线分别为AB=CD=$\sqrt{13}$，BC=DA=$\sqrt{10}$，AC=BD=$\sqrt{5}$，
    则$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}=13}\\{{a}^{2}+{b}^{2}=5}\\{{b}^{2}+{c}^{2}=10}\end{array}\right.$，解得a=2，b=1，c=3．
    ∴EF的长为c=3．
    故选：A．

    点评 本题考查棱锥的结构特征，考查了数形结合的解题思想方法，正确作出图形是解答该题的关键，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

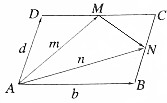    12．如图所示，平行四边形ABCD中，M为DC的中点，N是BC的中点，设$\overrightarrow{AB}$=$\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{d}$，$\overrightarrow{AM}$=$\overrightarrow{m}$，$\overrightarrow{AN}$=$\overrightarrow{n}$．
    （1）试以$\overrightarrow{b}$，$\overrightarrow{d}$为基底表示$\overrightarrow{MN}$；
    （2）试以$\overrightarrow{m}$，$\overrightarrow{n}$为基底表示$\overrightarrow{AB}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知z=a+bi（a、b∈R，i是虚数单位，$\overline{z_1}$是z的共轭复数），z1，z2∈C，定义D（z）=||z||=|a|+|b|，D（z1，z2）=||z1-z2||．现有三个命题：
    ①D（${\overline{z_1}}$）=D（z1）；       ②D（z1，z2）=D（z2，z1）；      ③λD（z1，z2）=D（λz1，λz2）．
    其中为真命题的是（　　）
    A．①②③B．①③C．②③D．①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．2x-1的值是否可以同时大于x-5和3x+1的值？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．（1）已知椭圆：$\frac{{x}^{2}}{9}$+y2=1，过左焦点F作倾斜角为$\frac{π}{6}$的直线交椭圆A、B两点，求弦AB的长；
    （2）已知椭圆4x2+y2=1及直线y=x+m，若直线被椭圆截得的弦长为$\frac{2\sqrt{10}}{5}$，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=x2+ax-lnx+1（a∈R），g（x）=x2-1
    （Ⅰ）当a=-1时，求函数y=f（x）的单调区间；
    （Ⅱ）设函数m（x）=f（x）-g（x），当x∈（0，e2]时，是否存在实数a，使得函数y=m（x）的最小值为4？若存在，求出a的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设函数f（x）=ax2-（2a-1）x-lnx，其中a∈R．
    （Ⅰ）当a＞0时，求函数f（x）的单调递增区间；
    （Ⅱ）当a＜0时，求函数f（x）在区间[$\frac{1}{2}$，1]上的最小值；
    （Ⅲ）记函数y=f（x）的图象为曲线C，设点A（x1，y1），B（x2，y2）是曲线C上不同的两点，点M为线段AB的中点，过点M作x轴的垂线交曲线C于点N，试判断曲线C在N处的切线是否平行于直线AB？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）=aex-x-1，a∈R．
    （Ⅰ）当a=1时，求f（x）的单调区间；
    （Ⅱ）当x∈（0，+∞）时，f（x）＞0恒成立，求a的取值范围；
    （Ⅲ）求证：当x∈（0，+∞）时，ln$\frac{{e}^{x}-1}{x}$＞$\frac{x}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．定义：若函数y=f（x）对定义域内的任意x，都有f（m+x）=f（m-x）恒成立，则称函数y=f（x）的图象的直线x=m对称，若函数f（x）=cx3+ax2+bx+1关于直线x=$\frac{1}{2}$对称，且a＞4（${\sqrt{e}$+1），则函数g（x）=ex+f（x）在下列区间内存在零点的是（　　）
    A．（-1，-$\frac{1}{2}}$）B．（-$\frac{1}{2}$，0）C．（$\frac{1}{2}$，1）D．（1，2）

    查看答案和解析>>

    同步练习册答案