
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
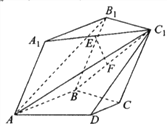
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)第(1)问,转化成证明![]() 平面
平面![]() ,再转化成证明
,再转化成证明![]() 和
和![]() .(2)第(2)问,先利用几何法找到
.(2)第(2)问,先利用几何法找到![]() 与平面
与平面![]() 所成角,再根据
所成角,再根据![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 求出
求出![]() 再建立空间直角坐标系,求出二面角
再建立空间直角坐标系,求出二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)连接![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 分别为
分别为![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() 平面
平面![]()
(2)设![]() ,由(1)得
,由(1)得![]() 平面
平面![]() .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() .
.
过点![]() 作
作![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,如图所示,
,如图所示,
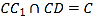
又![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
因为![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
由(1),得![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 是
是![]() 与平面
与平面![]() 所成角.
所成角.
因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,因为
,因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
所以![]() ,
, 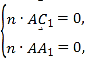 ,解得
,解得![]() .
.
在梯形![]() 中,易证
中,易证![]() ,分别以
,分别以![]() ,
, ![]() ,
, ![]() 的正方向为
的正方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由![]() ,及
,及![]() ,得
,得![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由![]() 得
得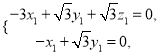 令
令![]() ,得m=(3,1,2)
,得m=(3,1,2)
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由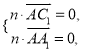 得
得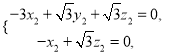 令
令![]() ,得
,得![]() .
.
所以![]()
又因为二面角![]() 是钝角,所以二面角
是钝角,所以二面角![]() 的余弦值是
的余弦值是![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】改革开放40多年来,城乡居民生活从解决温饱的物质需求为主逐渐转变到更多元化的精神追求,消费结构明显优化.下图给出了1983~2017年部分年份我国农村居民人均生活消费支出与恩格尔系数(恩格尔系数是食品支出总额占个人消费支出总额的比重)统计图.对所列年份进行分析,则下列结论错误的是( )
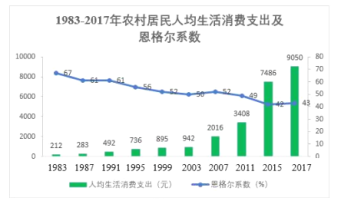
A.农村居民人均生活消费支出呈增长趋势
B.农村居民人均食品支出总额呈增长趋势
C.2011年至2015年农村居民人均生活消费支出增长最快
D.2015年到2017年农村居民人均生活消费支出增长比率大于人均食品支出总额增长比率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱长为4,过点
的底面边长为2,侧棱长为4,过点![]() 作平面
作平面![]() 与正四棱柱的三条侧棱
与正四棱柱的三条侧棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,且
,且![]() ,若多面体
,若多面体![]() 和多面体
和多面体![]() 的体积比为3∶5,则截面
的体积比为3∶5,则截面![]() 的周长为_________.
的周长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的单调性,并证明你的结论;
(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数a的值;
垂直,求实数a的值;
(2)若函数![]() 在
在![]() 上单调递增,求实数a的取值范围;
上单调递增,求实数a的取值范围;
(3)当![]() 时,若方程
时,若方程![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,
,![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
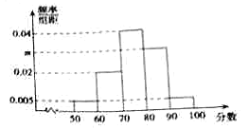
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校200名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
并通过计算判断,是否能在犯错误的概率不超过0.025的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出5人,进行体育锻炼体会交流,从参加体会交流的5人中,随机选出2人作重点发言,求恰好选出一名男生的概率.
参考公式: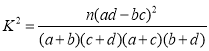 ,其中
,其中![]()
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
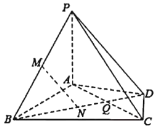
【题目】在三棱锥![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,底面
的中点,底面![]() 是正三角形,延长
是正三角形,延长![]() 到点
到点![]() ,使得
,使得![]() .
.
(1)![]() 为线段
为线段![]() 上确定一点,当
上确定一点,当![]() 平面
平面![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 平面
平面![]() ,且
,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com