
已知函数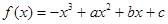 在
在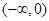 上是减函数,在
上是减函数,在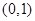 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且
上有三个零点,且 是其中一个零点.
是其中一个零点.
(1)求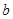 的值;
的值;
(2)求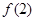 的取值范围;
的取值范围;
(3)设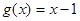 ,且
,且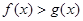 的解集为
的解集为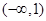 ,求实数
,求实数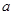 的取值范围.
的取值范围.
(1)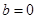 ,(2)
,(2)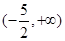 ,(3)
,(3)
解析试题分析:(1)函数在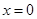 处单调性发生变化,所以
处单调性发生变化,所以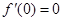 ,由
,由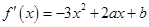 得
得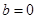 .(2)因为
.(2)因为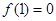 ,所以
,所以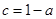 ,因此
,因此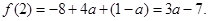 因为函数
因为函数 在
在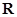 上有三个零点,所以
上有三个零点,所以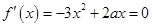 必有两个不等的根
必有两个不等的根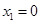 ,
,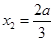 .又
.又 在
在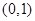 上是增函数,所以大根不小于1,即
上是增函数,所以大根不小于1,即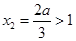 ,
,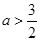 ,故
,故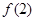 的取值范围为
的取值范围为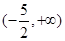 .(3)已知不等式解集求参数取值范围,有两个解题思路,一是解不等式,根据解集包含关系对应参数取值范围.二是转化,将不等式在区间有解理解为恒成立问题,利用函数最值解决参数取值范围.本题由于已知
.(3)已知不等式解集求参数取值范围,有两个解题思路,一是解不等式,根据解集包含关系对应参数取值范围.二是转化,将不等式在区间有解理解为恒成立问题,利用函数最值解决参数取值范围.本题由于已知 是其中一个零点,所以两个方法都简便.否则应利用变量分离求最值法.
是其中一个零点,所以两个方法都简便.否则应利用变量分离求最值法.
试题解析:(1)∵f(x)=-x3+ax2+bx+c,∴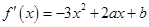 . 1分
. 1分
∵f(x)在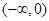 上是减函数,在
上是减函数,在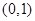 上是增函数,
上是增函数,
∴当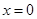 时,
时, 取到极小值,即
取到极小值,即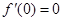 .∴
.∴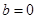 . 3分
. 3分
(2)由(1)知,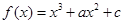 ,
,
∵ 是函数
是函数 的一个零点,即
的一个零点,即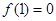 ,∴
,∴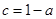 . 5分
. 5分
∵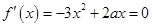 的两个根分别为
的两个根分别为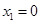 ,
,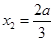 .
.
又∵ 在
在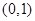 上是增函数,且函数
上是增函数,且函数 在
在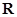 上有三个零点,
上有三个零点,
∴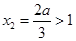 ,即
,即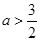 . 7分
. 7分
∴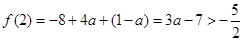 .
.
故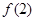 的取值范围为
的取值范围为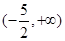 . 9分
. 9分
(3)解法1:由(2)知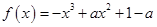 ,且
,且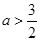 .
.
∵ 是函数
是函数 的一个零点,∴
的一个零点,∴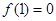 ,
,
∵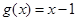 ,∴
,∴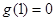 ,
,
∴点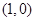 是函数
是函数 和函数
和函数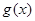 的图像的一个交点. 10分
的图像的一个交点. 10分
结合函数 和函数
和函数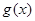 的图像及其增减特征可知,当且仅当函数
的图像及其增减特征可知,当且仅当函数 和函数
和函数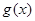 的图像只有一个交点
的图像只有一个交点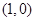 时,
时,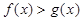 的解集为
的解集为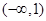 .
.
即方程组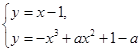 ①只有一组解:
①只有一组解: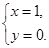 11分
11分
由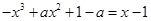 ,得
,得 .
.
即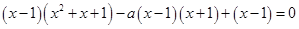 .
.
即

科目:高中数学 来源: 题型:解答题
已知某工厂生产 件产品的成本为
件产品的成本为 (元),
(元),
问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数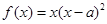 ,
,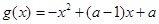 (其中
(其中 为常数).
为常数).
(1)如果函数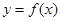 和
和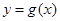 有相同的极值点,求
有相同的极值点,求 的值;
的值;
(2)设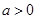 ,问是否存在
,问是否存在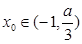 ,使得
,使得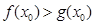 ,若存在,请求出实数
,若存在,请求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(3)记函数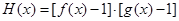 ,若函数
,若函数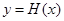 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商用一辆 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, 型卡车满载行驶时,每100km所消耗的燃油量
型卡车满载行驶时,每100km所消耗的燃油量 (单位:
(单位: )与速度
)与速度 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
(1)设运送这车水果的费用为 (元)(不计返程费用),将
(元)(不计返程费用),将 表示成速度
表示成速度 的函数关系式;
的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数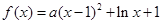 .
.
(1)当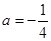 时,求函数
时,求函数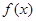 的极值;
的极值;
(2)若函数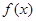 在区间
在区间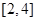 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(3)当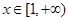 时,函数
时,函数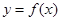 图像上的点都在
图像上的点都在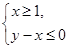 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com