
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.分析 (Ⅰ)过P作AD的垂线,垂足为O,根据平面PAD⊥平面ABCD,得PO⊥平面ABCD;再取AO中点M,连OG得到OG即为面EFG与面ABCD的交线;最后根据EM⊥平面ABCD.且OG⊥AO,得到的OG⊥EO求出∠EOM 即可.
(Ⅱ)由(Ⅰ)得PO⊥平面ABCD,故以O为原点,OG,OD,OP所在直线分别为x,y,z轴,建立空间直角坐标系,A(0,-2,0),B(4,-2,0),P(0,0,2$\sqrt{3}$),C(4,2,0)则E(0,-1,$\sqrt{3}$),F(2,-1,$\sqrt{3}$),$\overrightarrow{PC}=(4,2,-2\sqrt{3})$利用向量法求解.
解答 (Ⅰ)解:过P作AD的垂线,垂足为O,
∵平面PAD⊥平面ABCD,则PO⊥平面ABCD.
取AO中点M,连OG,EO,EM,∵EF∥AB∥OG,
∴OG即为面EFG与面ABCD的交线
又EM∥OP,则EM⊥平面ABCD.且OG⊥AO,
故OG⊥EO,∴∠EOM 即为所求
在RT△EOM中,EM=$\sqrt{3}$OM=1
∴tan∠EOM=$\sqrt{3}$,故∠EOM=60°
∴平面EFG与平面ABCD所成锐二面角的大小是60°.
(Ⅱ)解:由(Ⅰ)得PO⊥平面ABCD,
故以O为原点,OG,OD,OP所在直线分别为x,y,z轴,建立空间直角坐标系,
A(0,-2,0),B(4,-2,0),P(0,0,2$\sqrt{3}$),C(4,2,0)
则E(0,-1,$\sqrt{3}$),F(2,-1,$\sqrt{3}$),$\overrightarrow{PC}=(4,2,-2\sqrt{3})$
设面FEGO的法向量为$\overrightarrow{m}=(x,y,z)$
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{OE}=-x+\sqrt{3}z=0}\\{\overrightarrow{m}•\overrightarrow{OF}=2x-y+\sqrt{3}z=0}\end{array}\right.$可取$\overrightarrow{m}=(\sqrt{3},3\sqrt{3},1)$
设$\overrightarrow{PM}=λ\overrightarrow{PC}=(4λ,2λ,-2\sqrt{3}λ)$,(0≤λ≤1),
则$\overrightarrow{EM}=\overrightarrow{EP}+\overrightarrow{PM}=(0,1,\sqrt{3})$+(4λ,2λ,-2$\sqrt{3}λ$)=(4λ,2λ+1,$\sqrt{3}-2\sqrt{3}λ$)
由直线ME与平面EFG所成角的正弦值等于$\frac{\sqrt{6}}{4}$,得|cos$<\overrightarrow{m}$,$\overrightarrow{ME}$>|=$\frac{\sqrt{6}}{4}$,
即$\frac{8\sqrt{3}λ+4\sqrt{3}}{\sqrt{31}×\sqrt{32{λ}^{2}-8λ+4}}=\frac{\sqrt{6}}{4}$,可得120λ2-190λ-1=0,解得λ=$\frac{190±\sqrt{19{0}^{2}+480}}{2×120}$∉(0,1)
∴线段 PC上是不存在一点 M,使得直线ME与平面EFG所成角的正弦值等于$\frac{\sqrt{6}}{4}$.
点评 本题考查了空间角的求解,及动点问题的处理,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届湖北省协作校高三联考一数学(理)试卷(解析版) 题型:解答题
已知函数 的定义域为
的定义域为 ,
, ,函数
,函数 的值域为
的值域为 .
.
(1)当 时,求
时,求 ;
;
(2)是否存在实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年重庆市高一上学期第一次月考数学试卷(解析版) 题型:填空题
我们知道平方运算和开方运算是互逆运算,如: ,那么
,那么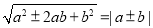 ,那么如何将双重二次根式
,那么如何将双重二次根式
 化简呢?如能找到两个数
化简呢?如能找到两个数
 ,使得
,使得 即
即 ,且使
,且使 即
即 ,那么
,那么
 ,双重二次根式得以化简;例如化简:
,双重二次根式得以化简;例如化简: ;
;  且
且 ,
,
 由此对于任意一个二次根式只要可以将其化成
由此对于任意一个二次根式只要可以将其化成 的形式,且能找到
的形式,且能找到 使得
使得 ,且
,且 ,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
(1)填空: _________________;
_________________; __________________;
__________________;
(2)化简:① ②
② (每题2分)
(每题2分)
(3)计算:
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 f(1)<f(2) | B. | 2 f(1)>f(2) | C. | 2 f(1)=f(2) | D. | f(1)=f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-5)∪(1,+∞) | B. | (1,19) | C. | [1,19) | D. | (19,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com