
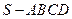 的底面是正方形,
的底面是正方形,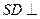 平面
平面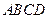 .
.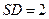 ,
,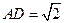 ,
,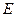 是
是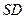 上的点.
上的点.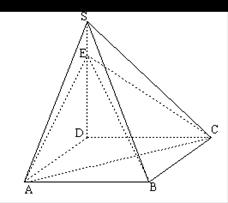
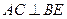 ;
;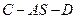 的余弦值.
的余弦值.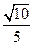
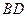 .
.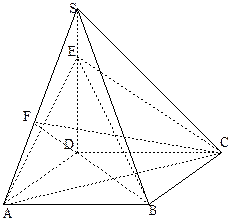
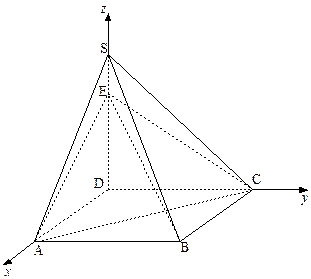
 是正方形,
是正方形,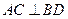 .
.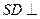 平面
平面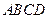 ,
,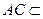 平面
平面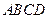 ,
,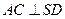 .……………………………………………………………………3分
.……………………………………………………………………3分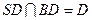 ,
,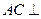 平面
平面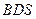 .……………………5分
.……………………5分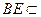 平面
平面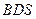 ,
,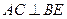 .…………………………7分
.…………………………7分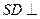 平面
平面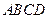 ,
,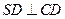 .
.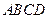 是正方形,
是正方形,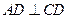 .
.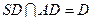 ,
,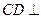 平面
平面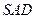 ,所以
,所以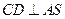 .…………………………………………10分
.…………………………………………10分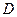 在平面
在平面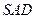 内作
内作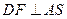 于
于 ,连结
,连结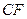 .
.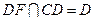 ,
,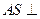 平面
平面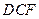 .
.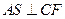 .
.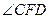 是二面角
是二面角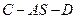 的平面角.………………………………………12分
的平面角.………………………………………12分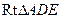 中,
中,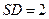 ,
,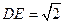 ,可求得
,可求得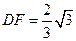 .
.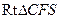 中,
中,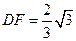 ,
,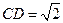 ,可求得
,可求得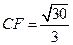 .
.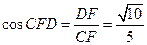 .
.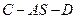 的余弦值为
的余弦值为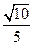 .…………………………………………14分
.…………………………………………14分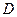 为原点建立空间直角坐标系
为原点建立空间直角坐标系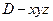 .
.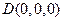 ,
,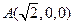 ,
,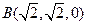 ,
,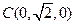 ,
,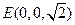 ,
,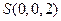 ,
,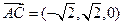 ,
, .…………………3分
.…………………3分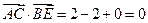 .
.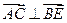 .即
.即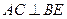 .…………………………………………………………7分
.…………………………………………………………7分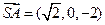 ,
,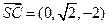 .
.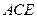 的法向量为
的法向量为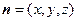 ,则由
,则由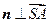 ,
,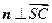 ,得
,得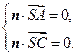 即
即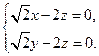
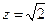 ,得
,得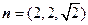 .……………………………………………………………11分
.……………………………………………………………11分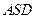 的一个法向量为
的一个法向量为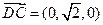 .
.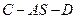 的平面角为
的平面角为 .
.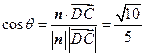 .
.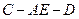 的余弦值为
的余弦值为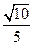 .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:不详 题型:解答题
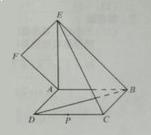
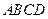 所在平面与平面四边形
所在平面与平面四边形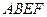 所在平面互相垂直,△
所在平面互相垂直,△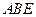 是等腰直角三角形,
是等腰直角三角形,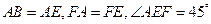 。
。
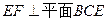 ;
;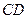 的中点为
的中点为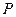 ,在直线
,在直线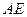 上是否存在一点
上是否存在一点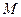 ,使得
,使得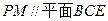 ?若存在,请指出点
?若存在,请指出点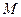 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;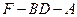 的大小。
的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
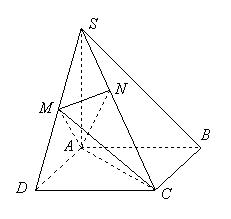
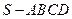 中,底面
中,底面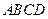 是正方形,
是正方形,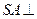 底面
底面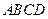 ,
,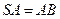 , 点
, 点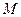 是
是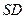 的中点,
的中点,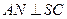 ,且交
,且交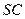 于点
于点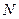 .
.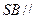 平面
平面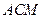 ;
;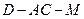 的余弦值大小;
的余弦值大小;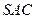 ⊥平面
⊥平面 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
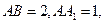
 直线
直线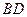 与平面
与平面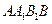 所成的角为
所成的角为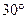 ,
,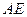 垂直
垂直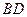 于
于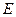 ,
,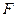 为
为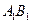 的中点.
的中点.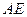 与
与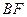 所成的角;
所成的角;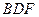 与平面
与平面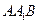 所成的二面角;
所成的二面角;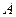 到平面
到平面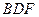 的距离.
的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
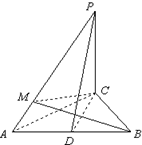
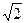 ,PB⊥PD.
,PB⊥PD.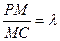 ,问
,问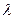 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.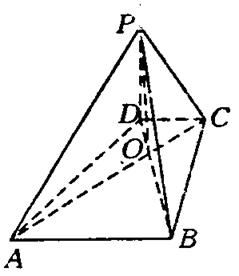
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com