
| A. | 2a+2c>2 | B. | 2a+2c≥2 | C. | 2a+2c≤2 | D. | 2a+2c<2 |
分析 运用分段函数的形式写出f(x)的解析式,作出f(x)=|2x-1|的图象,由题意可得c<0,a>0,2c<1且2a>1,且f(c)-f(a)>0,去掉绝对值,化简即可得到结论.
解答 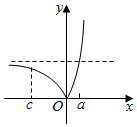 解:f(x)=|2x-1|=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{1-{2}^{x},x<0}\end{array}\right.$,
解:f(x)=|2x-1|=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{1-{2}^{x},x<0}\end{array}\right.$,
作出f(x)=|2x-1|的图象如图所示,
由图可知,要使c<b<a且f(c)>f(a)>f(b)成立,
则有c<0且a>0,
故必有2c<1且2a>1,
又f(c)-f(a)>0,即为1-2c-(2a-1)>0,
∴2a+2c<2.
故选:D.
点评 本题考查指数函数单调性的应用,考查用指数函数单调性确定参数的范围,本题借助函数图象来辅助研究,由图象辅助研究函数性质是函数图象的重要作用,以形助数的解题技巧必须掌握,是中档题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
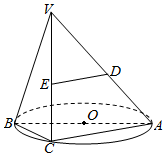 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.
如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
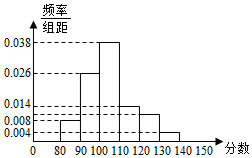 某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)
某中学一名高三数学教师,对其所教的文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | x | 0.1 | 0.2 | 2x | 0.1 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com