Question

4．已知圆O：x²+y²=1为△ABC的外接圆，且tanA=2，若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x+y的最大值为$\frac{5-\sqrt{5}}{4}$．

Answer 1

分析 延长AO交BC于D，设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$，（m＞0，n＞0），由平面向量基本定理和向量共线定理可得$\frac{m}{x}$=$\frac{n}{y}$=$\frac{|AD|}{|AO|}$，由B，C，D三点共线，可得$\frac{|AD|}{|AO|}$x+$\frac{|AD|}{|AO|}$y=1，进而得到x+y=$\frac{1}{1+\frac{|OD|}{|AO|}}$，求出|OD|的最小值，可过O作OM⊥BC，求得|OM|即可得到所求最大值．

解答 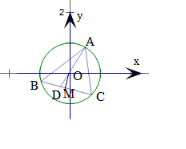解：延长AO交BC于D，设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$，（m＞0，n＞0），
又$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，易得$\frac{m}{x}$=$\frac{n}{y}$=$\frac{|AD|}{|AO|}$，
即有m=$\frac{|AD|}{|AO|}$x，n=$\frac{|AD|}{|AO|}$y，
则$\overrightarrow{AD}$=$\frac{|AD|}{|AO|}$x$\overrightarrow{AB}$+$\frac{|AD|}{|AO|}$y$\overrightarrow{AC}$，
由B，C，D三点共线，可得$\frac{|AD|}{|AO|}$x+$\frac{|AD|}{|AO|}$y=1，
即有x+y=$\frac{|AO|}{|AD|}$=$\frac{|AO|}{|AO|+|OD|}$=$\frac{1}{1+\frac{|OD|}{|AO|}}$，
由于|AO|=1，只需|OD|最小，
过O作OM⊥BC，垂足为M，则OD≥OM，
即有∠BOM=∠BAC，
由tan∠BAC=2，可得cos∠BAC=$\frac{\sqrt{5}}{5}$，
即有cos∠BAC=$\frac{|OM|}{|OB|}$=$\frac{\sqrt{5}}{5}$，则|OM|=$\frac{\sqrt{5}}{5}$．
则x+y≤$\frac{1}{1+\frac{\sqrt{5}}{5}}$=$\frac{5-\sqrt{5}}{4}$．
即有x+y的最大值为$\frac{5-\sqrt{5}}{4}$．
故答案为：$\frac{5-\sqrt{5}}{4}$．

点评 本题考查平面向量的基本定理的运用，主要考查向量共线定理的运用和同角的基本关系式的运用，考查运算能力，属于难题．