Question

16．已知复数z₁，z₂满足|z₁|≤1，-1≤Rez₂≤1，-1≤Imz₂≤1，若z=z₁+z₂，则z在复平面上对应的点组成的图形的面积为12+π．

Answer 1

分析 由题意设出z₁、z₂，结合z=z₁+z₂得到z的轨迹（x-a）²+（y-b）²=1，由圆心变化得到z所对应点的图形，则面积可求．

解答 解：∵复数z₁，z₂满足|z₁|≤1，-1≤Rez₂≤1，-1≤Imz₂≤1，
则可设z₁=cosθ+isinθ，z₂=a+bi（-1≤a≤1，-1≤b≤1），
由z=z₁+z₂，得z=（a+cosθ）+（b+sinθ）i，
设z=x+yi，则$\left\{\begin{array}{l}{x=a+cosθ}\\{y=b+sinθ}\end{array}\right.$，
∴（x-a）²+（y-b）²=1．
当a，b变化时，z点的轨迹如图：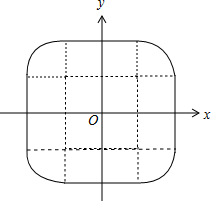

则z在复平面上对应的点组成的图形的面积为：
图中内部边长为2的正方形面积+四个长为2宽为1的长方形面积+四个四分之一圆的面积．
等于${2}^{2}+4×2×1+4×\frac{1}{4}π=12+π$．
故答案为：12+π．

点评 本题考查复数的代数表示法及其几何意义，考查数形结合的解题思想方法，关键是对题意的理解，属中档题．