
ЗжЮі ЃЈ1ЃЉШчЭМЫљЪОЃЌгЩ|PF1|+|PF2|=|QF1|=R=2$\sqrt{2}$ЃО|F1F2|=2ЃЌПЩЕУЖЏЕуPЕФЙьМЃЮЊЭждВЃЌЩшБъзМЗНГЬЮЊ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ЃЈaЃОbЃО0ЃЉЃЌa=$\sqrt{2}$ЃЌc=1ЃЌb2=a2-c2ЃЎМДПЩЕУГіЃЎ
ЃЈ2ЃЉЩшMЃЈx1ЃЌy1ЃЉЃЌNЃЈx2ЃЌy2ЃЉЃЎгЩ$\overrightarrow{OM}+2\overrightarrow{ON}=2\overrightarrow{O{F_1}}$ЃЌПЩЕУx1+2x2=-2ЃЌy1+2y2=0ЃЎАбx1=-2-2x2ЃЌy1=-2y2ЃЌДњШыЭждВЗНГЬПЩЕУ$\frac{ЃЈ2+2{x}_{2}ЃЉ^{2}}{2}+4{y}_{2}^{2}$=1ЃЌгж$\frac{{x}_{2}^{2}}{2}+{y}_{2}^{2}=1$ЃЌ
СЊСЂНтЕУМДПЩЕУГіЃЎ
ЃЈ3ЃЉМйЩшдкyжсЩЯДцдкЖЈЕуTЃЈ0ЃЌtЃЉЃЌЪЙвдABЮЊжБОЖЕФдВКуЙ§етИіЕуЃЎЩшжБЯпABЕФЗНГЬЮЊy=kx-$\frac{1}{3}$ЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎгыЭждВЗНГЬСЊСЂПЩЕУИљгыЯЕЪ§ЕФЙиЯЕЃЌДњШыЩЯЪН$\overrightarrow{TA}•\overrightarrow{TB}$=0ЃЌНтГіМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМЫљЪОЃЌЁп|PF1|+|PF2|=|QF1|=R=2$\sqrt{2}$ЃО|F1F2|=2ЃЌ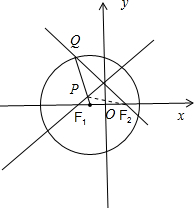
ЁрЖЏЕуPЕФЙьМЃЮЊЭждВЃЌЩшБъзМЗНГЬЮЊ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ЃЈaЃОbЃО0ЃЉЃЌa=$\sqrt{2}$ЃЌc=1ЃЌb2=1ЃЎ
ЁрЗНГЬCЮЊ$\frac{{x}^{2}}{2}+{y}^{2}$=1ЃЎ
ЃЈ2ЃЉЩшMЃЈx1ЃЌy1ЃЉЃЌNЃЈx2ЃЌy2ЃЉЃЎЁп$\overrightarrow{OM}+2\overrightarrow{ON}=2\overrightarrow{O{F_1}}$ЃЌ
Ёрx1+2x2=-2ЃЌy1+2y2=0ЃЎ
Ёрx1=-2-2x2ЃЌy1=-2y2ЃЌДњШыЭждВЗНГЬПЩЕУ$\frac{ЃЈ2+2{x}_{2}ЃЉ^{2}}{2}+4{y}_{2}^{2}$=1ЃЌгж$\frac{{x}_{2}^{2}}{2}+{y}_{2}^{2}=1$ЃЌ
СЊСЂНтЕУ$\left\{\begin{array}{l}{{x}_{2}=-\frac{5}{4}}\\{{y}_{2}=-\frac{\sqrt{14}}{8}}\end{array}\right.$ЃЌЁр$\left\{\begin{array}{l}{{x}_{1}=\frac{1}{2}}\\{{y}_{1}=\frac{\sqrt{14}}{4}}\end{array}\right.$ЃЎ
ЁрkMN=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{3\sqrt{14}}{14}$ЃЎ
ЃЈ3ЃЉМйЩшдкyжсЩЯДцдкЖЈЕуTЃЈ0ЃЌtЃЉЃЌЪЙвдABЮЊжБОЖЕФдВКуЙ§етИіЕуЃЎЩшжБЯпABЕФЗНГЬЮЊy=kx-$\frac{1}{3}$ЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎ
дђ$\overrightarrow{TA}•\overrightarrow{TB}$=ЃЈx1ЃЌy1-tЃЉ•ЃЈx2ЃЌy2-tЃЉ=x1x2+ЃЈy1-tЃЉЃЈy2-tЃЉ=x1x2+$ЃЈk{x}_{1}-\frac{1}{3}ЃЉЃЈk{x}_{2}-\frac{1}{3}ЃЉ$-t$[kЃЈ{x}_{1}+{x}_{2}ЃЉ-\frac{2}{3}]$+t2=ЃЈ1+k2ЃЉx1x2$-ЃЈ\frac{1}{3}k+tkЃЉ$ЃЈx1+x2ЃЉ+$\frac{1}{9}$+$\frac{2}{3}t$+t2=0ЃЌ
СЊСЂ$\left\{\begin{array}{l}{y=kx-\frac{1}{3}}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$ЃЌЛЏЮЊЃЈ1+2k2ЃЉx2-$\frac{4}{3}kx$-$\frac{16}{9}$=0ЃЌЁїЃО0КуГЩСЂЃЎ
Ёрx1+x2=$\frac{4k}{3ЃЈ1+2{k}^{2}ЃЉ}$ЃЌx1x2=-$\frac{16}{9ЃЈ1+2{k}^{2}ЃЉ}$ЃЎ
ДњШыЩЯЪНПЩЕУЃК-$\frac{16ЃЈ1+{k}^{2}ЃЉ}{9ЃЈ1+2{k}^{2}ЃЉ}$-$ЃЈ\frac{1}{3}k+ktЃЉЁС\frac{4k}{3ЃЈ1+2{k}^{2}ЃЉ}$+$\frac{1}{9}$+$\frac{2}{3}t$+t2=0ЃЌЛЏЮЊЃЈ18t2-18ЃЉk2+ЃЈ9t2+6t-15ЃЉ=0ЃЌ
Ёр$\left\{\begin{array}{l}{18{t}^{2}-18=0}\\{9{t}^{2}+6t-15=0}\end{array}\right.$ЃЌНтЕУt=1ЃЎТњзуЁїЃО0ЃЎ
ЁрдкyжсЩЯДцдкЖЈЕуTЃЈ0ЃЌ1ЃЉЃЌЪЙвдABЮЊжБОЖЕФдВКуЙ§етИіЕуTЃЎ
ЕуЦР БОЬтПМВщСЫЭждВЕФЖЈвхМАЦфБъзМЗНГЬЁЂжБЯпгыЭждВЯрНЛЮЪЬтзЊЛЏЮЊЗНГЬСЊСЂПЩЕУИљгыЯЕЪ§ЕФЙиЯЕЁЂдВЕФаджЪЁЂЯђСПзјБъдЫЫуЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкФбЬтЃЎ


 вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
вЛБОКУЬтПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2.44 | BЃЎ | 3.376 | CЃЎ | 2.376 | DЃЎ | 2.4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | Шє|$\overrightarrow{a}$|=0ЃЌдђ$\overrightarrow{a}$=0 | BЃЎ | Шє|$\overrightarrow{a}$|=|$\overrightarrow{b}$|ЃЌдђ$\overrightarrow{a}$=$\overrightarrow{b}$Лђ$\overrightarrow{a}$=-$\overrightarrow{b}$ | ||
| CЃЎ | Шє$\overrightarrow{a}$гы$\overrightarrow{b}$ЪЧЦНааЯђСПЃЌдђ|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | DЃЎ | Шє$\overrightarrow{a}$=$\overrightarrow{0}$ЃЌдђ-$\overrightarrow{a}$=$\overrightarrow{0}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {2} | BЃЎ | {$\sqrt{2}$} | CЃЎ | {-$\sqrt{2}$ЃЌ1ЃЌ$\sqrt{2}$ЃЌ2} | DЃЎ | {1ЃЌ$\sqrt{2}$ЃЌ2} |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com