考点:点、线、面间的距离计算,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)由AB
1∥D
1E,知∠AB
1C是异面直线D
1E与B
1C所成角(或所成角的补角),由此能求出异面直线D
1E与B
1C所成角的余弦值.
(2)以D为原点,DA为x轴,DC为y轴,DD
1为z轴,建立空间直角坐标系,利用向量法能求出A到直线B
1E的距离.
(3)求出平面D
1B
1E的法向量,利用向量法能求出直线AC与平面D
1EB
1所成的角.
(4)求出平面D
1B
1E的法向量和平面ACB
1的法向量利用向量法能求出两平面B
1D
1E与ACB
1所形成的锐二面角的余弦值.
(5)由
=(1,0,-1),平面D
1B
1E的法向量
=(2,-1,2),利用向量法能求出点A到平面D
1EB
1的距离.
解答:
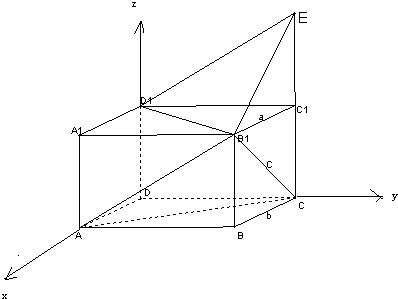
解:(1)∵E是长方体ABCD-A
1B
1C
1D
1的棱长CC
1所在直线上一点,
C
1E=CC
1=BC=
AB=1,
∴AB
1∥D
1E,
∴∠AB
1C是异面直线D
1E与B
1C所成角(或所成角的补角),
∵AB
1=
=
,
B1C==,
AC=
=
,
∴cos∠AB
1C=
=
.
∴异面直线D
1E与B
1C所成角的余弦值为
.
(2)以D为原点,DA为x轴,DC为y轴,
DD
1为z轴,建立空间直角坐标系,
由题意知A(1,0,0),
B
1(1,2,1),E(0,2,2),
∴
=(1,-2,-2),
=(1,0,-1),
∴A到直线B
1E的距离:
d=|
|•
=3×
=
.
(3)∵D
1(0,0,1),
E(0,2,2),C(0,2,0),
∴
=(1,2,0),
=(0,2,1),
=(-1,2,0),
设平面D
1B
1E的法向量
=(x,y,z),
则
,取x=2,得
=(2,-1,2),
设直线AC与平面D
1EB
1所成的角为θ,
则sinθ=|cos<
,>|=|
|=
.
∴直线AC与平面D
1EB
1所成的角为arcsin
.
(4)平面D
1B
1E的法向量
=(2,-1,2),
设平面ACB
1的法向量
=(a,b,c),
=(-1,2,0),
=(0,2,1),
则
,取b=1,得
=(2,1,-2),
两平面B
1D
1E与ACB
1所形成的锐二面角为α,
则cosα=|cos<
,>|=|
|=
.
∴两平面B
1D
1E与ACB
1所形成的锐二面角的余弦值为
.
(5)∵
=(1,0,-1),平面D
1B
1E的法向量
=(2,-1,2),
∴点A到平面D
1EB
1的距离:
d′=
=
=0.
点评:本题考查异面直线所成的角的余弦值、点到直线的距离、直线与平面所成的角、二面角的余弦值、点到平面的距离的求法,解题时要认真审题,注意向量法的合理运用.

 E是长方体ABCD-A1B1C1D1的棱长CC1所在直线上一点,C1E=CC1=BC=
E是长方体ABCD-A1B1C1D1的棱长CC1所在直线上一点,C1E=CC1=BC= 解:(1)∵E是长方体ABCD-A1B1C1D1的棱长CC1所在直线上一点,
解:(1)∵E是长方体ABCD-A1B1C1D1的棱长CC1所在直线上一点,

 快乐5加2金卷系列答案
快乐5加2金卷系列答案 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.点M是棱C1B1上的动点.