
分析 由已知条件得f′(x)=x2+|$\overrightarrow{a}$|x+$\overrightarrow{a}$•$\overrightarrow{b}$=0成立,△=|$\overrightarrow{a}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$>0,由此能求出$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的取值范围.
解答 解:∵关于x的函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$|$\overrightarrow{a}$|x2+$\overrightarrow{a}$•$\overrightarrow{b}$x在R上有极值,
∴f′(x)=x2+|$\overrightarrow{a}$|x+$\overrightarrow{a}$•$\overrightarrow{b}$=0成立,方程有根,
△=|$\overrightarrow{a}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$>0,
∴|$\overrightarrow{a}$|2-4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ>0,
由|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0,得cosθ$<\frac{1}{2}$,
∴$\frac{π}{3}$<θ<π
故答案为:($\frac{π}{3}$,π).
点评 本题考查向量的夹角的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x-y-3=0 | D. | x-y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
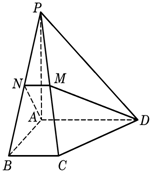 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.
如图,椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和双曲线C2:$\frac{{x}^{2}}{4}$-y2=1有公共顶点A,B,P,Q分别在C1,C2且异于A,B点.直线AP,BP,AQ,BQ的斜率分别为k1,k2,k3,k4且k1+k2+k3+k4=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
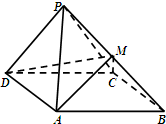 如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,∠ADC=60°,点P在底面ABCD上的射影为△ACD的重心,点M为线段PB上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E为BC的中点.
如图四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com