
分析 (Ⅰ)先利用两角和公式和对函数解析式化简整理,根据图象的平移确定g(x)的解析式,根据x的范围和三角函数的图象与性质确定g(x)的最大值的解析式,求得m.
(Ⅱ)根据第一问中函数的解析式确定B的值,进而利用余弦定理和基本不等式确定b的范围,最后确定周长的范围.
解答 解:(Ⅰ)由题设得$f(x)=sin2x-cos2x-1+m=\sqrt{2}sin(2x-\frac{π}{4})-1+m$,
∴$g(x)=\sqrt{2}sin[2(x+\frac{π}{4})-\frac{π}{4}]-1+m=\sqrt{2}sin(2x+\frac{π}{4})-1+m$,
因为当$x∈[0,\frac{π}{4}]$时,$2x+\frac{π}{4}∈[\frac{π}{4},\frac{3π}{4}]$,
所以由已知得$2x+\frac{π}{4}=\frac{π}{2}$,即$x=\frac{π}{8}$时,$g{(x)_{max}}=\sqrt{2}+m-1=\sqrt{2}$,
所以m=1;
(Ⅱ)由已知$g(\frac{3}{4}B)=\sqrt{2}sin(\frac{3}{2}B+\frac{π}{4})=1$,
因为三角形中$0<\frac{3}{2}B<\frac{3π}{2}$,
所以$\frac{π}{4}<\frac{3}{2}B+\frac{π}{4}<\frac{7π}{4}$,
所以$\frac{3}{2}B+\frac{π}{4}=\frac{3π}{4}$,即$B=\frac{π}{3}$,
又因为a+c=2,由余弦定理得:${b^2}={a^2}+{c^2}-2accosB={a^2}+{c^2}-ac={(a+c)^2}-3ac≥{(a+c)^2}-\frac{{3{{(a+c)}^2}}}{4}=1$,
当且仅当a=c=1时等号成立,
又∵b<a+c=2,∴1≤b<2,
所以△ABC的周长l=a+b+c∈[3,4),
故△ABC的周长l的取值范围是[3,4).
点评 本题主要考查了三角函数图象与性质,余弦定理的应用.考查了学生综合分析问题的能力和一定的推理能力.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{41}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{4\sqrt{41}}{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3]∪[4,+∞) | B. | [3,4] | C. | (-∞,3] | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
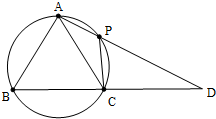 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com