

���� �����ɼ�У����Ƶ���ֲ�����ͼ�����a������У����Ƶ�ʷֲ�����ͼ�����b��
���������������������У��ƽ��ֵ����У��ƽ��ֵ��
�������������ݿ�֪��ѵ��5���м�У��2�ˣ��ֱ����E��F����У��3�ˣ��ֱ����M��N��Q����5������ѡ2�ˣ������оٷ��������������ͬһѧУ�ĸ��ʣ�
��� �⣺���߲��Գɼ��Ӹߵ������η�ΪA��B��C��D�ĸ��ȼ���
��������˼ס�������ѧУ��60��ѧ���ijɼ���
���ɼ�У����Ƶ���ֲ�����ͼ֪��
6+a+33+6=60�����a=15��
����У����Ƶ�ʷֲ�����ͼ�ã�0.15+b+0.2+0.15=1�����b=0.5��
���������ݿɵü�У��ƽ��ֵΪ$\overline{{x}_{��}}$=$\frac{90��6+80��15+60��33+50��6}{60}$=67��
��У��ƽ��ֵΪ$\overline{{x}_{��}}$=90��0.15+80��0.5+60��0.2+50��0.15=73��
�������������ݿ�֪��ѵ��5���м�У��2�ˣ��ֱ����E��F����У��3�ˣ��ֱ����M��N��Q��
��5������ѡ2�ˣ�һ����10�������¼����ֱ�Ϊ��
EF��EM��EN��EQ��FM��FN��FQ��MN��MQ��NQ��
����2 ������ͬһѧУ������EF��MN��MQ��NQ��
����������ͬһѧУ�ĸ���p=$\frac{4}{10}=\frac{2}{5}$��
���� ���⿼��Ƶ�ʷֲ�ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 6 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | �� | ||||||||||||
| 8 | 9 | 9 | 8 | 9 | 9 | 3 | 8 | 9 | 9 | ||||
| 2 | 0 | 1 | 0 | 4 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | ||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Vp����q | B�� | �V��p��q�� | C�� | ���Vp����q | D�� | p�ģ��Vq�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 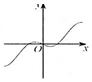 | B�� | 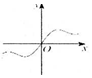 | C�� | 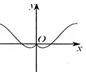 | D�� | 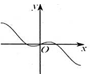 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 210 | B�� | 190 | C�� | 220 | D�� | 242 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
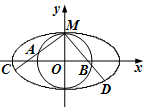 ��ͼ��ԲO��������Ϊ$\frac{{\sqrt{3}}}{2}$����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$��a��b��0�������ڵ�M��0��1����
��ͼ��ԲO��������Ϊ$\frac{{\sqrt{3}}}{2}$����Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$��a��b��0�������ڵ�M��0��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com