
已知函数f(x)=sin2ωx+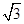 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,
(Ⅰ)求ω的值及函数f(x)的单调增区间;
(Ⅱ)求函数f(x)在[0,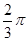 ]上的值域.
]上的值域.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
某单位有 、
、 、
、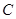 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为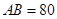
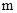 ,
,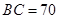
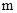 ,
,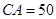
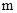 .假定
.假定 、
、 、
、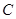 、
、 四点在同一平面上.
四点在同一平面上.
(1)求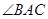 的大小;
的大小;
(2)求点 到直线
到直线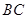 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com