
分析 (1)曲线ρ=2(0<θ<π),即ρ2=4,(0<θ<π),化为直角坐标方程:x2+y2=4(0<y≤2).设线段AP的中点Q(x,y),A(x′,y′),则$x=\frac{2+{x}^{′}}{2}$,y=$\frac{{y}^{′}}{2}$,解得x′=2x-2,y′=2y.代入方程(x′)2+(y′)2=4,即可得出.
(2)轨迹C的方程为:y=$\sqrt{1-(x-1)^{2}}$=$\sqrt{2x-{x}^{2}}$,设M(x0,y0).y′=$\frac{1-x}{\sqrt{2x-{x}^{2}}}$,根据迹C上的点M处的切线斜率的取值范围是[-$\sqrt{3}$,-$\frac{\sqrt{3}}{3}$],可得$-\sqrt{3}$≤$\frac{1-{x}_{0}}{\sqrt{2{x}_{0}-{x}_{0}^{2}}}$≤$-\frac{\sqrt{3}}{3}$,解出即可得出.
解答 解:(1)曲线ρ=2(0<θ<π),即ρ2=4,(0<θ<π),化为直角坐标方程:x2+y2=4(0<y≤2).
设线段AP的中点Q(x,y),A(x′,y′),则$x=\frac{2+{x}^{′}}{2}$,y=$\frac{{y}^{′}}{2}$,解得x′=2x-2,y′=2y.
∵(x′)2+(y′)2=4,∴(2x-2)2+(2y)2=4,化为:(x-1)2+y2=1.
由y′∈(0,2],可得0<2y≤2,解得0<y≤1.
∴点Q的轨迹C的直角坐标方程:(x-1)2+y2=1(0<y≤1).
(2)轨迹C的方程为:y=$\sqrt{1-(x-1)^{2}}$=$\sqrt{2x-{x}^{2}}$,设M(x0,y0).
y′=$\frac{(2x-{x}^{2})^{′}}{2\sqrt{2x-{x}^{2}}}$=$\frac{1-x}{\sqrt{2x-{x}^{2}}}$,
∵迹C上的点M处的切线斜率的取值范围是[-$\sqrt{3}$,-$\frac{\sqrt{3}}{3}$],
∴$-\sqrt{3}$≤$\frac{1-{x}_{0}}{\sqrt{2{x}_{0}-{x}_{0}^{2}}}$≤$-\frac{\sqrt{3}}{3}$,
解得:$\frac{3}{2}$≤x0≤$\frac{2+\sqrt{3}}{2}$.
∴点M横坐标的取值范围是$[\frac{3}{2},\frac{2+\sqrt{3}}{2}]$.
点评 本题考查了极坐标方程化为直角坐标方程、利用导数研究曲线切线的斜率、坐标变换,考查了推理能力与计算能力,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
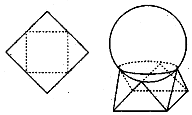 如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )
如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{\sqrt{6}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | 3 | C. | $\frac{24}{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$ | B. | $3\overrightarrow{DF}$ | C. | $\overrightarrow{BF}$ | D. | $\frac{3}{2}\overrightarrow{BF}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com