
分析 (1)根据函数f(x) 的图象经过点(-$\frac{1}{2}$,-1),可得loga(1-$\frac{1}{4}$)=-1,求得a的值.
(2)由于函数f(x)=${log}_{\frac{4}{3}}$(1-x2) 为偶函数,再利用f($\frac{1}{2}$)=f(-$\frac{1}{2}$),计算求的结果.
解答 解:(1)函数f(x)=loga(1+x)-loga(1-x)=loga(1-x2) 的图象经过点(-$\frac{1}{2}$,-1),
∴loga(1-$\frac{1}{4}$)=-1,求得a=$\frac{4}{3}$.
(2)由于函数f(x)=${log}_{\frac{4}{3}}$(1-x2) 为偶函数,f($\frac{1}{2}$)=f(-$\frac{1}{2}$)=-1.
点评 本题主要考查对数的运算性质,函数的奇偶性的判断,属于基础题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
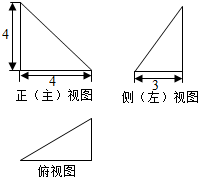
| A. | $2\sqrt{34}$ | B. | $8\sqrt{2}$ | C. | 10 | D. | $6\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 9 | C. | 5或9 | D. | 10或18 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
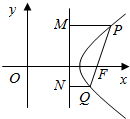 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com