
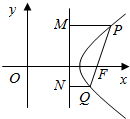
 如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小.
如图,点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,过点F的直线的斜率为3,与双曲线交于P,Q两点,分别过P、Q向右准线作垂线,垂足分别为M,N,且$\overrightarrow{PM}$=3$\overrightarrow{QN}$,求双曲线的离心率的大小. 分析 设|$\overrightarrow{PM}$|=3|$\overrightarrow{QN}$|=3m.由双曲线定义得,|PF|=3me.|QF|=me.过Q做QA垂直于PM,垂足Q,根据直线的斜率可知|AQ|=6m,进而利用勾股定理求得e.
解答 解:设|$\overrightarrow{PM}$|=3|$\overrightarrow{QN}$|=3m.由双曲线定义得,|PF|=3me.|QF|=me.过Q做QA垂直于PM,垂足Q.
∵过点F的直线的斜率为3,|AP|=2m.
∴|AQ|=6m,
∴(2m)2+(6m)2=(4me)2,
∴e=$\frac{\sqrt{10}}{2}$.
点评 本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和解决问题的能力.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0) | C. | $(-∞,-\frac{1}{5})$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=(x-1)$\sqrt{\frac{1+x}{1-x}}$ | B. | f(x)=$\frac{|x|}{x}$ | ||
| C. | f(x)=$\left\{\begin{array}{l}{1+x,(x≥0)}\\{1-x(x<0)}\end{array}\right.$ | D. | f(x)=$\frac{1}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com