Question

13．已知P为抛物线y²=3x上的一个动点，Q为圆$C：{（x+\frac{1}{4}）^2}+{（y-1）^2}=\frac{1}{16}$上一个动点，点P到y轴距离为d，则|PQ|+d的最小值为$\sqrt{2}-1$．

Answer 1

分析 设抛物线焦点为F，根据抛物线的性质可知d=|PF|-1，连结CF，则d+|PQ|的最小值为|CF|-1，求解即可．

解答 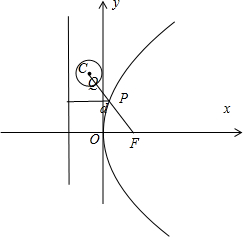解：∵抛物线的准线方程为x=-$\frac{3}{4}$，焦点F（$\frac{3}{4}$，0）．
P到直线x=-$\frac{3}{4}$的距离等于|PF|，
∴P到y轴的距离d=|PF|-$\frac{3}{4}$，|PQ|=|PC|-$\frac{1}{4}$
∴d+|PQ|=|PF|+|PC|-$\frac{3}{4}$$-\frac{1}{4}$．
∴当F，P，Q三点共线时，|PF|+|PQ|取得最小值|CF|-1．
圆$C：{（x+\frac{1}{4}）^2}+{（y-1）^2}=\frac{1}{16}$上一个动点，
∵C（-$\frac{1}{4}$，1），F（$\frac{3}{4}$，0），∴|CF|=$\sqrt{2}$，
∴d+|PQ|的最小值为$\sqrt{2}$-1．
故答案为：$\sqrt{2}-1$．

点评 本题考查了抛物线的性质，两点间的距离公式，属于中档题．