
分析 (1)使用二倍角公式计算cosB;
(2)利用余弦定理求出ac的最大值,根据三角形的面积求出高.
解答 解:(I)在△ABC中,∵cos2B-$\sqrt{3}$cos(A+C)=2,
∴2cos2B-1+$\sqrt{3}$cosB=2,解得cosB=$\frac{\sqrt{3}}{2}$或cosB=-$\sqrt{3}$(舍).
∴B=$\frac{π}{6}$.
(2)由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-4}{2ac}=\frac{\sqrt{3}}{2}$,
∴a2+c2=4+$\sqrt{3}$ac≥2ac,解得ac≤4(2+$\sqrt{3}$).
∴S=$\frac{1}{2}acsinB$=$\frac{1}{4}ac$≤2+$\sqrt{3}$.
又∵S=$\frac{1}{2}bh$≤2+$\sqrt{3}$,∴h≤2+$\sqrt{3}$.
∴AC边上高h的最大值为2+$\sqrt{3}$.
点评 本题考查了三角函数的恒等变换,余弦定理在解三角形中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
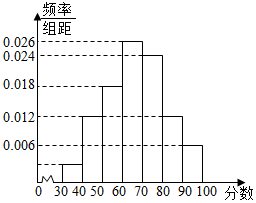 某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在[80,100]的学生可取得A等(优秀),在[60,80)的学生可取得B等(良好),在[40,60)的学生可取得C等(合格),在不到40分的学生只能取得D等(不合格),为研究这次考试成绩优秀是否与性别有关,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按从低到高分成[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100]七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com