
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,及点
,及点![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率不为![]() 的动直线
的动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,记
两点,记![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,试求
,试求![]() (
(![]() 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得出关于![]() 、
、![]() 的方程组,可求出
的方程组,可求出![]() 、
、![]() 的值,进而可求得
的值,进而可求得![]() 的值,由此可得出椭圆
的值,由此可得出椭圆![]() 的方程;
的方程;
(2)解法一:设点![]() 、
、![]() 、
、![]() ,将点
,将点![]() 、
、![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程,变形后相减可得
的方程,变形后相减可得 ,再由
,再由![]() 、
、![]() ,经过向量的坐标运算求得
,经过向量的坐标运算求得![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 内得到
内得到![]() ,再由三角形的面积公式可求得
,再由三角形的面积公式可求得![]() 面积的取值范围;
面积的取值范围;
解法二:设点![]() 、
、![]() 、
、![]() ,由
,由![]() 、
、![]() ,根据向量的坐标运算得出
,根据向量的坐标运算得出![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 的方程联立,由
的方程联立,由![]() 得出
得出![]() 的取值范围,由
的取值范围,由![]() 代入韦达定理并消去
代入韦达定理并消去![]() ,得出
,得出![]() ,进而得出
,进而得出![]() ,再由三角形的面积公式可求得
,再由三角形的面积公式可求得![]() 面积的取值范围;
面积的取值范围;
解法三:设直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 的方程联立,由
的方程联立,由![]() 得出
得出![]() 的取值范围,并列出韦达定理,利用向量的线性运算可得出
的取值范围,并列出韦达定理,利用向量的线性运算可得出![]() ,并求出原点
,并求出原点![]() 到直线
到直线![]() 的距离,利用三角形的面积公式可求得
的距离,利用三角形的面积公式可求得![]() 面积的取值范围.
面积的取值范围.
(1)依题意 ,解得
,解得 ,
,![]() ,
,
所以椭圆![]() 的方程是
的方程是![]() ;
;
(2)解法一:
设![]() 、
、![]() 、
、![]() ,则
,则 ,
,
相减得:![]()
![]() ,
,
又由![]() ,知
,知![]() ,
,![]() ,
,
由![]() ,知
,知![]() ,
,![]() ,
,
代入![]() 式得:
式得:![]() ,即
,即![]() ,
,
又因为点![]() 在椭圆内,所以
在椭圆内,所以![]() ,
,
所以![]() 的面积
的面积![]() ;
;
解法二:设![]() ,
,![]() ,
,![]() ,则
,则 ,
,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 的方程得:
的方程得:
![]() ,由
,由![]() 得
得![]() ,
,![]() .
.
所以 ,消去
,消去![]() 得到
得到![]() ,
,
所以 ,
,
因此![]() 的面积
的面积![]() ;
;
解法三:设直线![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 的方程得:
的方程得:
![]() ,由
,由![]() 得
得![]() ,
,![]() .
.
所以 ,
,![]() ,
,
![]() ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() 的面积
的面积![]() ,
,
因为![]() ,所以
,所以 .
.


科目:高中数学 来源: 题型:
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况,调查部门在该校进行了一次问卷调查(共12道题),从该校学生中随机抽取40人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如下频率分布直方图.
六组,得到如下频率分布直方图.
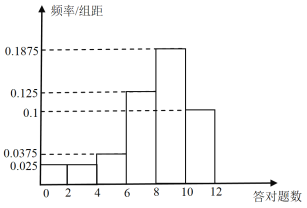
(1)若答对一题得10分,未答对不得分,估计这40人的成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB=AC=![]() ,BC=AA1=2,O,M分别为BC,AA1的中点.
,BC=AA1=2,O,M分别为BC,AA1的中点.
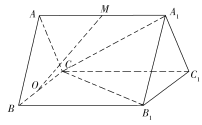
(1)求证:OM∥平面CB1A1;
(2)求点M到平面CB1A1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱![]() 的底面边长为2,侧棱长为4,过点
的底面边长为2,侧棱长为4,过点![]() 作平面
作平面![]() 与正四棱柱的三条侧棱
与正四棱柱的三条侧棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,且
,且![]() ,若多面体
,若多面体![]() 和多面体
和多面体![]() 的体积比为3∶5,则截面
的体积比为3∶5,则截面![]() 的周长为_________.
的周长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”…江南梅雨的点点滴滴都流露着浓烈的诗情.每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南![]() 镇2009~2018年梅雨季节的降雨量(单位:
镇2009~2018年梅雨季节的降雨量(单位:![]() )的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
)的频率分布直方图,试用样本频率估计总体概率,解答下列问题:

(1)计算![]() 的值,并用样本平均数估计
的值,并用样本平均数估计![]() 镇明年梅雨季节的降雨量;
镇明年梅雨季节的降雨量;
(2)![]() 镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅这10年的亩产量(
镇的杨梅种植户老李也在犯愁,他过去种植的甲品种杨梅,亩产量受降雨量的影响较大(把握超过八成).而乙品种杨梅这10年的亩产量(![]() /亩)与降雨量的发生频数(年)如
/亩)与降雨量的发生频数(年)如![]() 列联表所示(部分数据缺失).请你完善
列联表所示(部分数据缺失).请你完善![]() 列联表,帮助老李排解忧愁,试想来年应种植哪个品种的杨梅受降雨量影响更小?并说明理由.
列联表,帮助老李排解忧愁,试想来年应种植哪个品种的杨梅受降雨量影响更小?并说明理由.
亩产量\降雨量 | 200~400之间 | 200~400之外 | 合计 |
| 2 | ||
| 1 | ||
合计 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
(参考公式:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数a的值;
垂直,求实数a的值;
(2)若函数![]() 在
在![]() 上单调递增,求实数a的取值范围;
上单调递增,求实数a的取值范围;
(3)当![]() 时,若方程
时,若方程![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,
,![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对时下的“抖音热”某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() ,若有
,若有![]() 的把握认为是否喜欢抖音和性别有关则调查人数中男生可能有( )人
的把握认为是否喜欢抖音和性别有关则调查人数中男生可能有( )人
附表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附:
A.20B.40C.60D.80
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com