
【题目】
已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆否命题为:“若
”的逆否命题为:“若 ![]() ,则
,则 ![]() ”
”
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.若 ![]() 且
且 ![]() 为假命题,则
为假命题,则 ![]() 、
、 ![]() 均为假命题
均为假命题
D.命题 ![]() :“
:“ ![]() ,使得
,使得 ![]() ”,则
”,则 ![]() :“
:“ ![]() ,均有
,均有 ![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知曲线C1的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若 ![]() ,则
,则 ![]() 或
或 ![]() ;
;
② ![]() ,都有
,都有 ![]() ;
;
③若 ![]() 是实数,则
是实数,则 ![]() 是
是 ![]() 的充分不必要条件;
的充分不必要条件;
④“ ![]() ” 的否定是“
” 的否定是“ ![]() ” ;
” ;
其中真命题的个数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距![]() ,汽车从甲地行驶到乙地,速度不得超过
,汽车从甲地行驶到乙地,速度不得超过![]() ,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (
(![]() )的平方成正比,比例系数为
)的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (
(![]() )的函数,指出定义域;
)的函数,指出定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水仙花经营部每天的房租、水电、人工等固定成本为1000元,每盆水仙花的进价是10元,销售单价![]() (元) (
(元) (![]() )与日均销售量
)与日均销售量![]() (盆)的关系如下表,并保证经营部每天盈利.
(盆)的关系如下表,并保证经营部每天盈利.
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
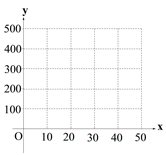
(Ⅰ) 在所给的坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定
的对应点,并确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(Ⅲ)请写出该经营部的日销售利润![]() 的表达式,并回答该经营部怎样定价才能获最大日销售利润?
的表达式,并回答该经营部怎样定价才能获最大日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ,且
,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)将函数 ![]() 的图像向右平移
的图像向右平移 ![]() 个单位长度得到函数
个单位长度得到函数 ![]() 的图像,若函数
的图像,若函数 ![]() 在
在 ![]() 上有零点,求
上有零点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com