
设函数f(θ)=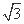 sin θ+cos θ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sin θ+cos θ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为(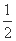 ,
,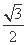 ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω:  上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
如图所示,在正△ABC中,点D,E分别在边AC, AB上,且AD=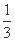 AC,
AC,
AE=  AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
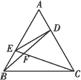
(1)求证:A,E,F,D四点共圆;
(2)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有 ≤f
≤f ,已知函数y=sin x在区间
,已知函数y=sin x在区间
(0,π)上是凸函数,则在△ABC中,sin A+sin B+sin C的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(cos x,- 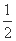 ),b=(
),b=(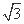 sin x,cos 2x),x∈R,设函数f(x)=a·b.
sin x,cos 2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在[0,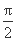 ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数y=sin2x+2cos x( ≤x≤
≤x≤ )的最大值与最小值分别为( )
)的最大值与最小值分别为( )
(A)最大值为 ,最小值为-
,最小值为-
(B)最大值为 ,最小值为-2
,最小值为-2
(C)最大值为2,最小值为-
(D)最大值为2,最小值为-2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,
当x∈(0, )时,f(x)=sin πx,f
)时,f(x)=sin πx,f =0,则函数f(x)在区间[0,6]上的零点个数是( )
=0,则函数f(x)在区间[0,6]上的零点个数是( )
(A)3 (B)5 (C)7 (D)9
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C:  +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )
(A)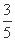 (B)
(B)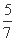 (C)
(C) (D)
(D)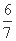
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com