
| A. | (0,1] | B. | [1,2) | C. | [0,1] | D. | [1,2] |
分析 求出A,B集合,根据集合的基本运行性质,求出∁RA,再求B∩∁RA.
解答 解:由题意:A={x|$\frac{x-2}{x}$>0}={x|x>2或x<0},
那么:∁RA={x|0≤x≤2},
由题意可知B={y|y=5-4t-$\frac{1}{t}$,t>0},
∵y=5-(4t+$\frac{1}{t}$),t>0.
4t+$\frac{1}{t}$$≥2\sqrt{4t•\frac{1}{t}}=4$当且仅当t=$\frac{1}{2}$是取等号.
∴y≤1
故得B={y|y≤1}.
则B∩∁RA={x|0≤x≤1},
故选C.
点评 本题考查了集合的基本运算与不等式的结合.属于基础题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | ∅∈A | B. | $\sqrt{3}$∉A | C. | $\sqrt{3}$∈A | D. | {$\sqrt{3}$}∈A. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数且最小正周期为$\frac{π}{2}$ | B. | 奇函数且最小正周期为$\frac{π}{2}$ | ||
| C. | 偶函数且最小正周期为π | D. | 奇函数且最小正周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0]∪[2,+∞) | B. | [0,1] | C. | (-∞,0]∪(2,+∞) | D. | (-∞,1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
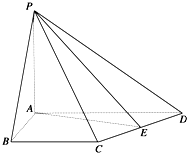 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=4,BC=3,AD=5,PA=4,∠DAB=∠ABC=90°,E是CD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=4,BC=3,AD=5,PA=4,∠DAB=∠ABC=90°,E是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com