
分析 (Ⅰ)利用cos2θ+sin2θ=1,可把曲线C的参数方程可化为普通方程;直线l的方程为ρsin(θ+$\frac{π}{4}$)=$\sqrt{2}$.可化为 $\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=$\sqrt{2}$,
,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出直线l的直角坐标方程.
(Ⅱ)令y=0,得x=2,即M点的坐标为(2,0).又曲线c为圆,圆C的圆心坐标为(1,2),半径r=1,则|MC|=$\sqrt{5}$.利用|MN|≤|MC|+r即可得出.
解答 解:(Ⅰ)利用cos2θ+sin2θ=1,可把曲线C的参数方程可化为(x-1)2+(y-2)2=1,
直线l的方程为ρsin(θ+$\frac{π}{4}$)=$\sqrt{2}$.可化为 $\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=$\sqrt{2}$,
可得:直线l的直角坐标方程为 x+y-2=0.
(Ⅱ)令y=0,得x=2,即M点的坐标为(2,0).
又曲线c为圆,圆C的圆心坐标为(1,2),半径r=1,则|MC|=$\sqrt{5}$.
∴|MN|≤|MC|+r=$\sqrt{5}$+1,
∴|MN|的最大值为$\sqrt{5}+$1.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$tan35° | D. | tan35° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
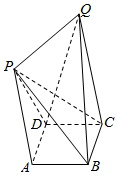 如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.
如图,在四棱锥P-ABCD中.底面ABCD为矩形,侧棱PA⊥平面ABCD,AP∥CQ,AB=2BC=2,CQ=$\frac{3}{2}$AP=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | $\frac{4}{5}$ | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com