Question

5．已知函数f（x）满足f（x）=x³+ax²-x+c（c＞0），且$a=f'（\frac{2}{3}）$
（Ⅰ）求a的值；
（Ⅱ）若方程f（x）=0有且只有两个不等的实根，求常数c；
（Ⅲ）在（Ⅱ）的条件下，求曲线f（x）与直线g（x）=x+1围成封闭图形的面积．

Answer 1

分析 （Ⅰ）先求导，再代值计算即可；
（Ⅱ）当$f（-\frac{1}{3}）=0$或f（1）=0时，f（x）=0有且只有两个不等的实根，即可求出c的值，
（Ⅲ）根据定积分在几何中的应用即可求出

解答 （Ⅰ）解：∵f（x）=x³+ax²-x+c，f'（x）=3x²+2ax-1，
令$x=\frac{2}{3}$得：$f'（\frac{2}{3}）=3{（\frac{2}{3}）^2}+2f'（\frac{2}{3}）•\frac{2}{3}-1$，解得$f'（\frac{2}{3}）=-1$，
即a=-1先判断函数的单调性，再根据
（Ⅱ）由f（x）=x³-x²-x+c得f'（x）=3x²-2x-1=（3x+1）（x-1）

x	$（{-∞，-\frac{1}{3}}）$	$-\frac{1}{3}$	$（-\frac{1}{3}，1）$	1	（1，+∞）
f'（x）	+	0	-	0	+
f（x）	↗	极大值	↘	极小值	↗

∴当$f（-\frac{1}{3}）=0$或f（1）=0时，f（x）=0有且只有两个不等的实根．
即$c+\frac{5}{27}=0$或c-1=0，
∵c＞0，
∴c=1，
（Ⅲ）由f（x）=g（x）得，x³-x²-x+1=x+1，
解得：x=-1，0，2
所以曲线f（x）与直线g（x）=x+1围成封闭图形的面积$S=\int_{-1}^0{（{x^3}-{x^2}-2x）}dx-\int_0^2{（{x^3}-{x^2}-2x）}dx=\frac{37}{12}$．

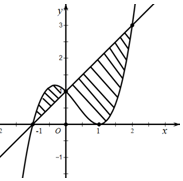
点评 本题考查了导数和函数的单调性以及方程根的问题，考查了定积分的应用，属于中档题