
分析 由条件利用同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)∵tanα=3,∴$\frac{3sinα-2cosα}{sinα-cosα}$=$\frac{3tanα-2}{tanα-1}$=$\frac{9-2}{3-1}$=$\frac{7}{2}$;
(2)∵tanα=3,∴$\frac{1}{si{n}^{2}α-co{s}^{2}α}$=$\frac{{sin}^{2}α{+cos}^{2}α}{{sin}^{2}α{-cos}^{2}α}$=$\frac{{tan}^{2}α+1}{{tan}^{2}α-1}$=$\frac{9+1}{9-1}$=$\frac{5}{4}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.


科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数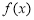 的定义域为
的定义域为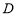 ,若对任意
,若对任意 ,当
,当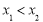 时,都有
时,都有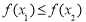 ,则称函数
,则称函数 在
在 上为非减函数.设函数
上为非减函数.设函数 在
在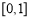 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③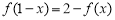 .则
.则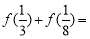 ( )
( )
A. 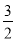 B.
B. 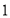 C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [$\frac{1}{10}$,10] | C. | [$\frac{1}{10}$,+∞) | D. | (0,10) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com