
分析 通过函数表达式可知f(x)表示点(a2+2,a2+2)与圆x2+y2=a2上点连线的斜率,且斜率最大与最小的临界值是直线与圆相切的时候,联立直线与圆的方程,利用△=0,通过韦达定理即得结论.
解答 解:∵f(x)=$\frac{{a}^{2}+asinx+2}{{a}^{2}+acosx+2}$=$\frac{{a}^{2}+2-(-asinx)}{{a}^{2}+2-(-acosx)}$(x∈R)
∴f(x)表示点(a2+2,a2+2)与圆x2+y2=a2上点连线的斜率,
∴斜率最大与最小的临界值是直线与圆相切的时候,即△=0,
联立$\left\{\begin{array}{l}{y=k(x-{a}^{2}-2)+{a}^{2}+2}\\{{x}^{2}+{y}^{2}={a}^{2}}\end{array}\right.$,
消去x整理得:(1+k2)x2+2k(1-k)(a2+2)x+(1-k)2(a2+2)2-a2=0,
令△=0,即[2k(1-k)(a2+2)]2=4(1+k2)[(1-k)2(a2+2)2-a2],
整理得:[(a2+2)2-a2]k2-2(a2+2)2k+(a2+2)2-a2=0,
由韦达定理可知:M(a)•m(a)=$\frac{({a}^{2}+2)^{2}-{a}^{2}}{({a}^{2}+2)^{2}-{a}^{2}}$=1,
故答案为:1.
点评 本题考查函数的最值及其几何意义,考查数形结合能力,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
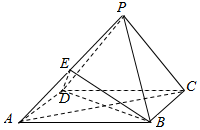 如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.
如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 4或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 26 | C. | 25 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
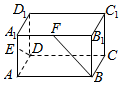 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com