
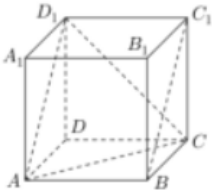
 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题:| A. | ①③ | B. | ①③④ | C. | ①②④ | D. | ③④ |
分析 ①由正方体的性质可得:BC1∥AD1,于是BC1∥平面AD1C,可得直线BC1上的点到平面AD1C的距离不变,而△AD1C的面积不变,即可判断出结论.
②由①可知:直线BC1上的点到平面AD1C的距离不变,而AP的大小在改变,可得直线AP与平面ACD1所成角的大小改变,即可判断出正误.
③由①可知:点P到平面AD1C的距离不变,点P到AD1的距离不变,即可判断出二面角P-AD1-C的大小是否改变.
④如图所示,不妨设正方体的棱长为a,设P(x,y,0),利用|PD|=|PC1|,利用两点之间的距离公式化简即可得出.
解答 解:①由正方体的性质可得:BC1∥AD1,于是BC1∥平面AD1C,因此直线BC1上的点到平面AD1C的距离不变,点P在直线BC1上运动,又△AD1C的面积不变,因此三棱锥A-D1PC的体积=$\frac{1}{3}{d}_{P}•{S}_{△A{D}_{1}C}$不变.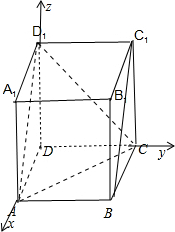
②点P在直线BC1上运动,由①可知:直线BC1上的点到平面AD1C的距离不变,而AP的大小在改变,因此直线AP与平面ACD1所成角的大小改变,故不正确.
③点P在直线BC1上运动,由①可知:点P到平面AD1C的距离不变,点P到AD1的距离不变,可得二面角P-AD1-C的大小不变,
正确;
④如图所示,不妨设正方体的棱长为a,D(0,0,0),C1(0,a,a),设P(x,y,0),∵|PD|=|PC1|,则$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}+(y-a)^{2}+{a}^{2}}$,化为y=a,因此P的轨迹是过点B的直线,正确.
其中的真命题是①③④.
故选:B.
点评 本题考查了空间位置关系、三棱锥的体积、空间角,考查了空间想象能力、推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com